Two sides of a rhombus ABCD are parallel to the lines y = x + 2 and y = 7x + 3 If the diagonals of the rhombus intersect at the point (1, 2) and the vertex A is on the y-axis, then vertex A can be a. (0,3) b. (0,5/2) c. (0,0) d. (0,6)
(0,3)
(0,5/2)
(0,0)
(0,6)
The correct Answer is:B, C
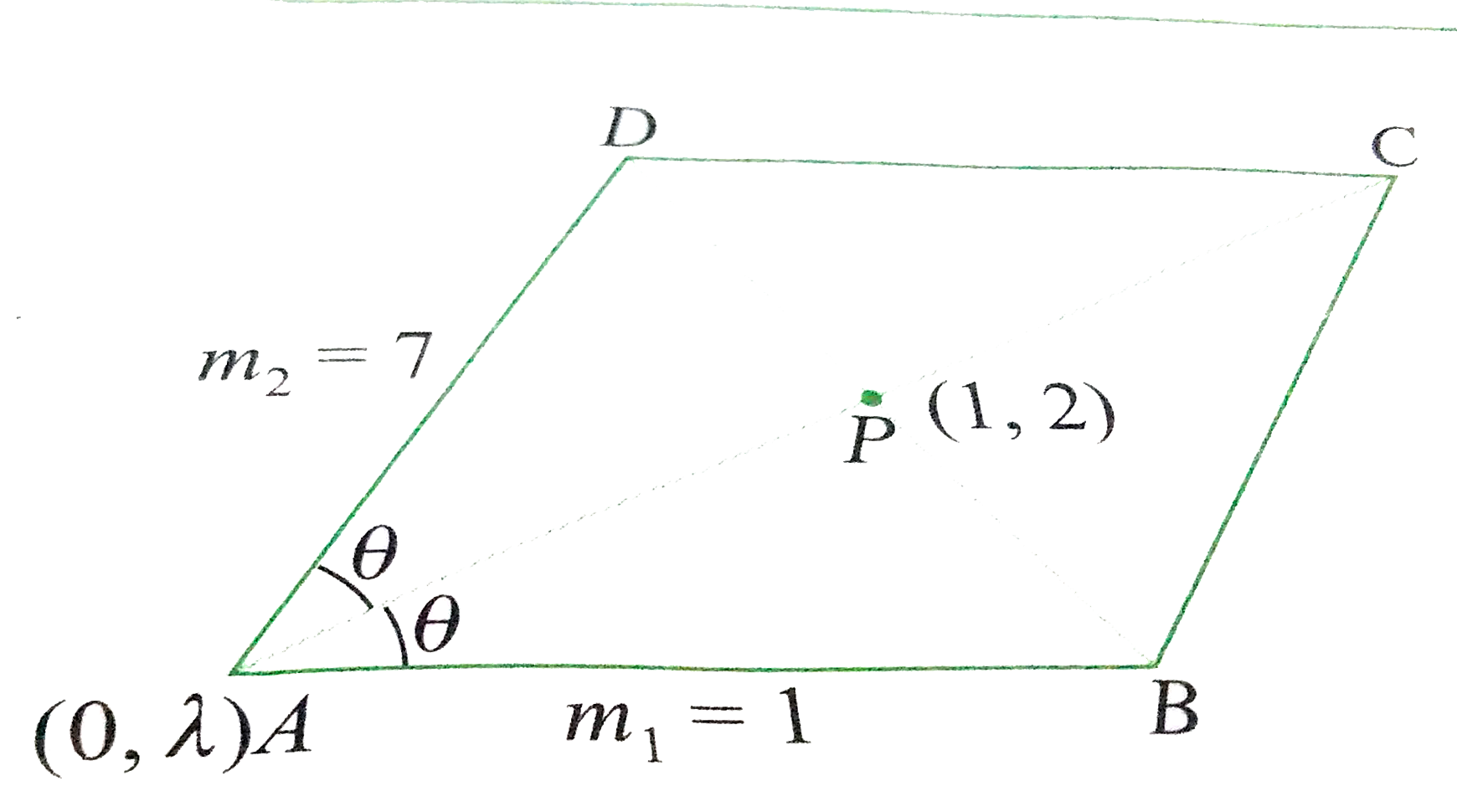
Let point A be (0,λ)
Slope of AP=λ−20−1=2−λ
AB and AC are parallel to the lines y=x+2 and y=7x+3respectively.
Thus, slope of AB and AC are 1 and 7, respectively.
From the figure,
tanθ=(2−λ)−11+(2−λ)=7−(2−λ)1+7(2−λ)
⇒(1−λ3−λ)=(5+λ15−7λ)
⇒(λ−1)(7λ−15)=(5+λ)(3−λ)
⇒8λ20λ=0
A=(0,0)and(0,5/2) .
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Linked
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Matrix match type
4 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Exercises
59 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Two sides of a Rhombus ABCD are parallel to the lines x−y=5 and 7x−y=3. The diagonals intersect at (2,1) then the equations of the diagonals are
View SolutionThe sides of a rhombus are parallel to the lines x+y−1=0 and 7x−y−5=0. It is given that the diagonals of the rhombus intersect at (1, 3) and one vertex, A of the rhombus lies on the line y=2x . Then the coordinates of vertex A are
(a)(85,165) (b) (715,1415) (c)(65,125) (d) (415,815)
View SolutionThe sides of a rhombus are parallel to the lines x+y−1=0 and 7x−y−5=0. It is given that the diagonals of the rhombus intersect at (1, 3) and one vertex, A of the rhombus lies on the line y=2x . Then the coordinates of vertex A are (85,165) (b) (715,1415) (65,125) (d) (415,815)
View Solutionthe equation of two adjacent sides of rhombus are given by y=x and y=7x. the diagonals of the rhombus intersect each other at point of (1,2).then the area of the rhombus is:
View SolutionThe sides of a rhombus are parallel to y=2x+3and2y=x+5 . The diagonals of the rhombus intersect at (1, 2). If one vertex of the rhombus lies on the y-axis then possible values of the ordinates of this vertex are 1 (b) 2 (c) 3 (d) 4
View SolutionA rhombus has two of its sides parallel to the lines y=2x+3andy=7x+2. If the diagonals cut at (1, 2) and one vertex is on the y-axis, find the possible values of the coordinate of that vertex.
View SolutionTwo sides of a rhombus are along the lines,x−y+1=0 and 7x−y−5=0 . If its diagonals intersect at (−1,−2) , then which one of the following is a vertex of this rhombus ? (1) (−3,−9) (2) (−3,−8) (3) (13,−83) (4) (−103,−73)
View SolutionTwo sides of a rhombus lying in the first quadrant are given by 3x−4y=0 and 12x−5y=0. If the length of the longer diagonal is 12, then find the equations of the other two sides of the rhombus.
View SolutionFind the equation of the parabola whose focus is at (0, 0) and vertex is at the intersection of the line x+y=1andx−y=3.
View SolutionIf the two sides of rhombus are x+2y+2=0 and 2x+y−3=0, then find the slope of the longer diagonal.
View Solution
