Let cos−1(4x3−3x)=a+bcos−1x
If x∈[−1,−12), then the value of a+bπ is
A
−π3
B
π3
C
−π6
D
π6
Video Solution
Text Solution
The correct Answer is:A
Let cos−1x=θ or x=cosθ, where θ∈[0,π]
cos−1(4x3−3x)=cos−1(4cos3θ−3cosθ)=cos−1(cos3θ)=cos−1(cosα)
where α=3θ∈[0,3π]
Refer to the graph of y=cos−1(cosα),α∈[0,3π]
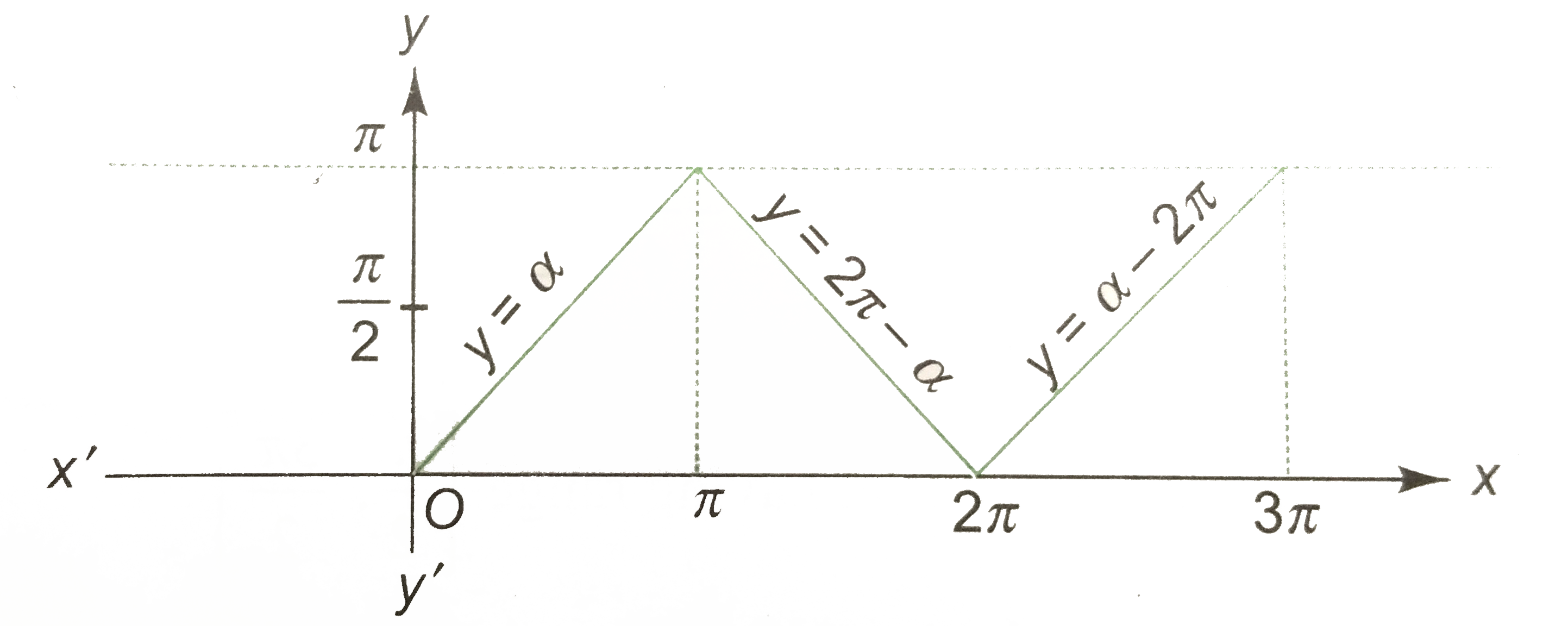
From the graph,
cos−1(4x3−3x)=cos−1(cosα)
=⎧⎪⎨⎪⎩α0≤α<π2π−απ≤α≤2πα−2π2π<α≤3π
=⎧⎪⎨⎪⎩3cos−1x0≤3cos−1x<π2π−3cos−1xπ≤3cos−1x≤2π3cos−1x−2π2π<3cos−1x≤3π
=⎧⎪⎨⎪⎩3cos−1x0≤3cos−1x<π2π−3cos−1x(π≤3)cos−1x≤(2π/3)3cos−1x−2π(2π/3)<cos−1x≤π
=⎧⎪
⎪⎨⎪
⎪⎩3cos−1x(1/2)<x≤12π−3cos−1x(−1/2)≤x≤(1/2)3cos−1x−2π−1≤x<−(−1/2)
=⎧⎪
⎪⎨⎪
⎪⎩3cos−1x−2π−1≤x<(−1/2)2π−3cos−1x(−1/2)≤x≤(1/2)3cos−1x(1/2)<x≤1
For x∈[−1,−12),cos∧(−1)(4x3−3x)=3cos−1x−2π
⇒a=−2πandb=3⇒a+bπ=π
For x∈[−12,12],cos−1(4x3−3x)=2π−3cos−1x
⇒a=2πandb=−3
⇒sin−1(sin.ab)=sin−1(sin.2π−3)=sin−1(−√32)=−π3
For x∈(12,1],cos−1(4x3−3x)=3cos−1x
→a=0andb=3
∴lomy→abcos(y)=limy→03cos(y)=3
|
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONSBook:CENGAGE ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Matrix match type
Explore 8 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:CENGAGE ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Numerical value type
Explore 18 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:CENGAGE ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Multiple correct answer type
Explore 24 Videos
- INTRODUCTION TO VECTORS Book:CENGAGE ENGLISHChapter:INTRODUCTION TO VECTORS Exercise:MATRIX-MATCH TYPE
Explore 3 Videos
- JEE 2019Book:CENGAGE ENGLISHChapter:JEE 2019Exercise:Chapter 10
Explore 9 Videos
Similar Questions
Let cos−1(4x3−3x)=a+bcos−1x
If x∈(12,1], then the value of limy→abcos(y) is
View SolutionLet cos−1(4x3−3x)=a+bcos−1x
Q. If x∈[−12,12], then sin−1(sinab) is :
View SolutionDefine y=cos−1(4x3−3x) in terms of cos−1x
View SolutionIf cos−1x=π3, the find the value of sin−1x.
View SolutionDifferentiate cos−1(4x3−3x) with respect to x , if x∈(−1, −12)
View SolutionDifferentiate cos−1(4x3−3x) with respect to x , if x∈(−12,12)
View SolutionLet cos(2tan−1x)=12 then the value of x is
View SolutionDifferentiate cos−1(4x3−3x) with respect to x , if x∈(12, 1)
View SolutionIf sin−1x=π4, find the value of cos−1x.
View SolutionIf the domain of the function f(x)=√3cos−1(4x)−π is [a,b], then the value of (4a+64b) is ___
View Solution
