The solution of the inequality log2sin−1x>log1/2cos−1x is
x∈[0,π√2]
x∈(1√2,1]
x∈(0,1√2)
none of these
The correct Answer is:C
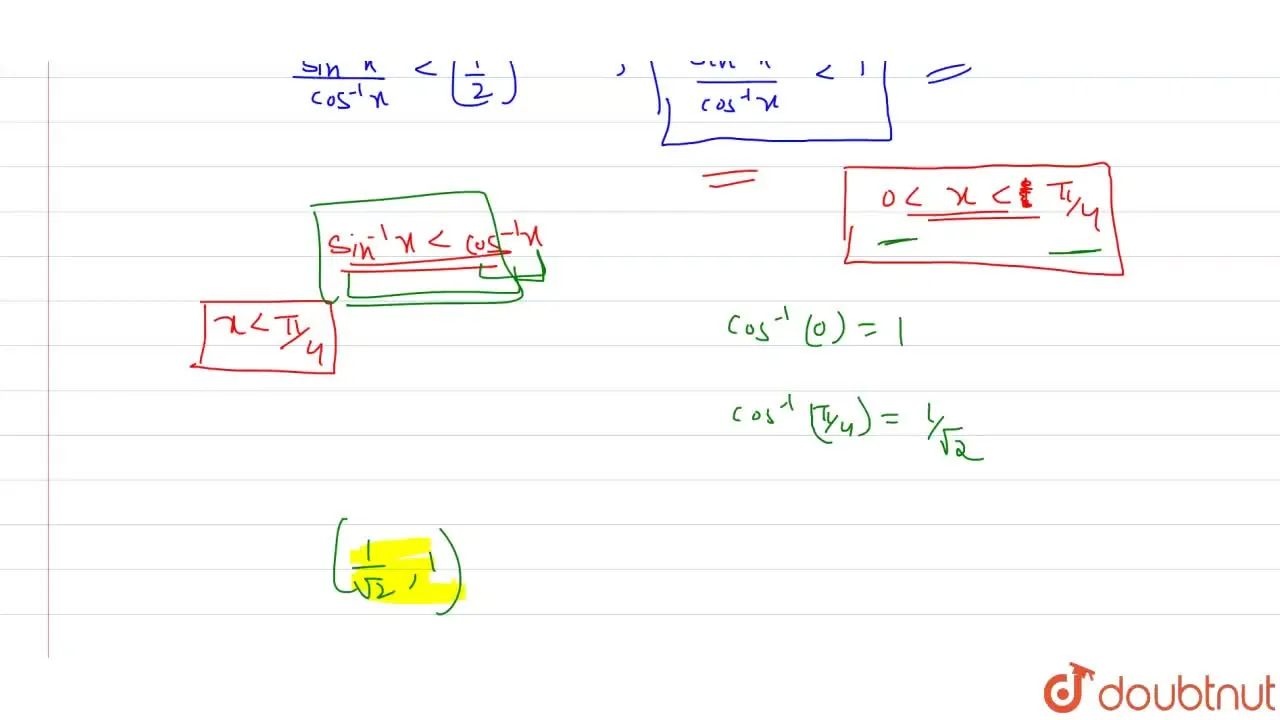
log1/2sin−1x>log1/2cos−1x
⇒cos−1x>sin−1x,0<x<1
⇒cos−1x>π2−cos−1x,0<x<1
⇒cos−1x>(π)/(4),0<x<1
⇒0<x<1√2
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Multiple correct answer type24videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Linked comprehension type16videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Concept application exercise 7.69videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - MATRIX-MATCH TYPE3videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
Similar Questions
The solution of the inequality log1/2sinx>log1/2cosx is
View SolutionThe solution of the inequality (log)12sin−1x>(log)1/2cos−1x is x∈[0,1√2] (b) x∈[1√2,1] x∈(0,1√2) (d) none of these
View SolutionThe solution set of the inequation
log1/2sinx>log1/2cosxin[0,2π], isView SolutionThe solution of the equation
logcosxsinx+logsinxcosx=2 is given byView SolutionSolve the inequality: log1/2(x+1)>log2(2−x)
View Solutionlog(sin−1x)
View SolutionThe solution of the equation logcosx2(3−2x)<logcosx2(2x−1) is:
View SolutionThe solution set of the inequation ∣∣∣2x−1x−1∣∣∣>2, is
View SolutionStatement-1: The solution set of the equation logx2×log2x2=log4x2is{2−√2,2√2}. Statement-2 : logba=1logab and logaxy=logax+logay
View SolutionThe number of real solutions of the equation log(−x)=2log(x+1), is
View Solution