Two sides of a triangle are parallel to the coordinate axes. If the slopes of the medians through the acute angles of the triangle are 2 and m, then m is (a)12 (b) 2 (c) 4 (d) 8
a. 1/2
b. 2
c. 4
d. 8
The correct Answer is:A, D
m1=Slope of AD=−a2b
m2=Slope of BE=−2ab
∴m1m2=14
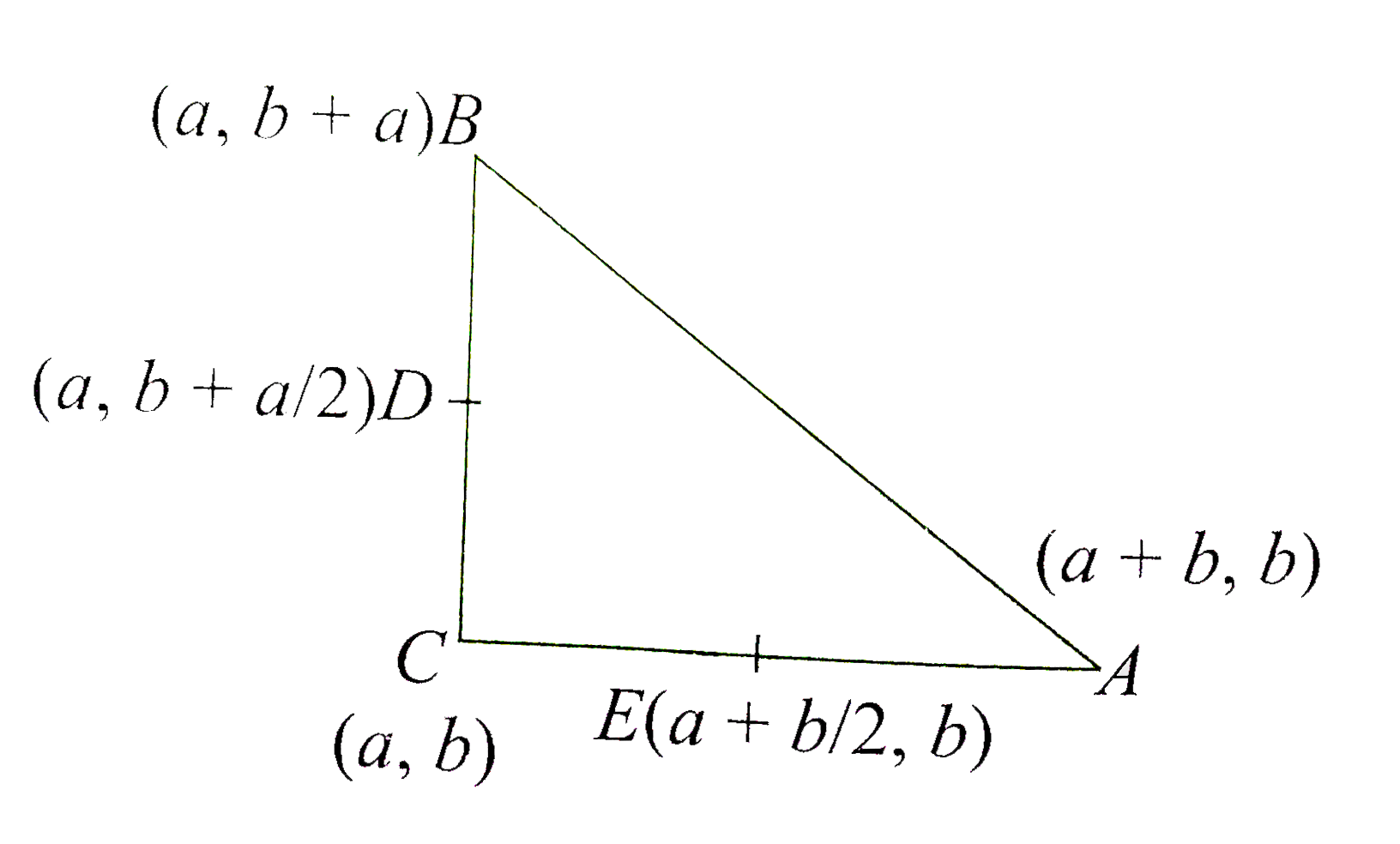
If m1=2, then m2=m=8
If m2=2,then m1=m=1/2.
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (LINKED COMPREHENSION TYPE)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (MATRIX MATCH TYPE)
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:EXERCISE (SINGLE CORRECT ANSWER TYPE)
Explore 82 Videos
- STRAIGHT LINEBook:CENGAGE ENGLISHChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGE ENGLISHChapter:THEORY OF EQUATIONSExercise:JEE ADVANCED (Numerical Value Type )
Explore 1 Video
Similar Questions
The lengths of the medians through acute angles of a right-angled triangle are 3 and 4. Find the area of the triangle.
View SolutionTwo sides of a triangle are along the coordinate axes and the medians through the vertices (other than the origin) are mutually perpendicular. The number of such triangles is/are (a) zero (b) two (c) four (d) infinite
View SolutionA (4,8), B(-2,6) are two vertices of a triangle ABC. Find the coordinates of C if the centroid of the triangle is (2,7).
View SolutionTwo medians drawn from the acute angles of a right angled triangle intersect at an angle π6. If the length of the hypotenuse of the triangle is 3 units, then the area of the triangle (in sq. units) is (a) √3 (b) 3 (c) √2 (d) 9
View SolutionIn an acute angled triangle , express a median in term of its sides.
View SolutionTwo medians drawn from the acute angles of a right angled triangle intersect at an angle π6. If the length of the hypotenuse of the triangle is 3units, then the area of the triangle (in sq. units) is √3 (b) 3 (c) √2 (d) 9
View SolutionLet ABC be an isosceles triangle with AB=BC. If base BC is parallel to x-axis and m1andm2 are the slopes of medians drawn through the angular points BandC, then
View SolutionFind the locus of the circumcenter of a triangle whose two sides are along the coordinate axes and the third side passes through the point of intersection of the line ax+by+c=0 and lx+my+n=0.
View SolutionIf the plane x2+y3+z4=1 cuts the coordinate axes in A,B,C, then the area of triangle ABC is
View SolutionIn an acute triangle ABC , if the coordinates of orthocentre H are (4,b) , of centroid G are (b,2b−8) and of circumcenter S are (−4,8) , then b cannot be (a) 4 (b) 8 (c) 12 (d) −12
View Solution

