The center of a square is at the origin and its one vertex is A(2,1). Find the coordinates of the other vertices of the square.
The correct Answer is:(-2,1), (-1,2) and (1,-2)
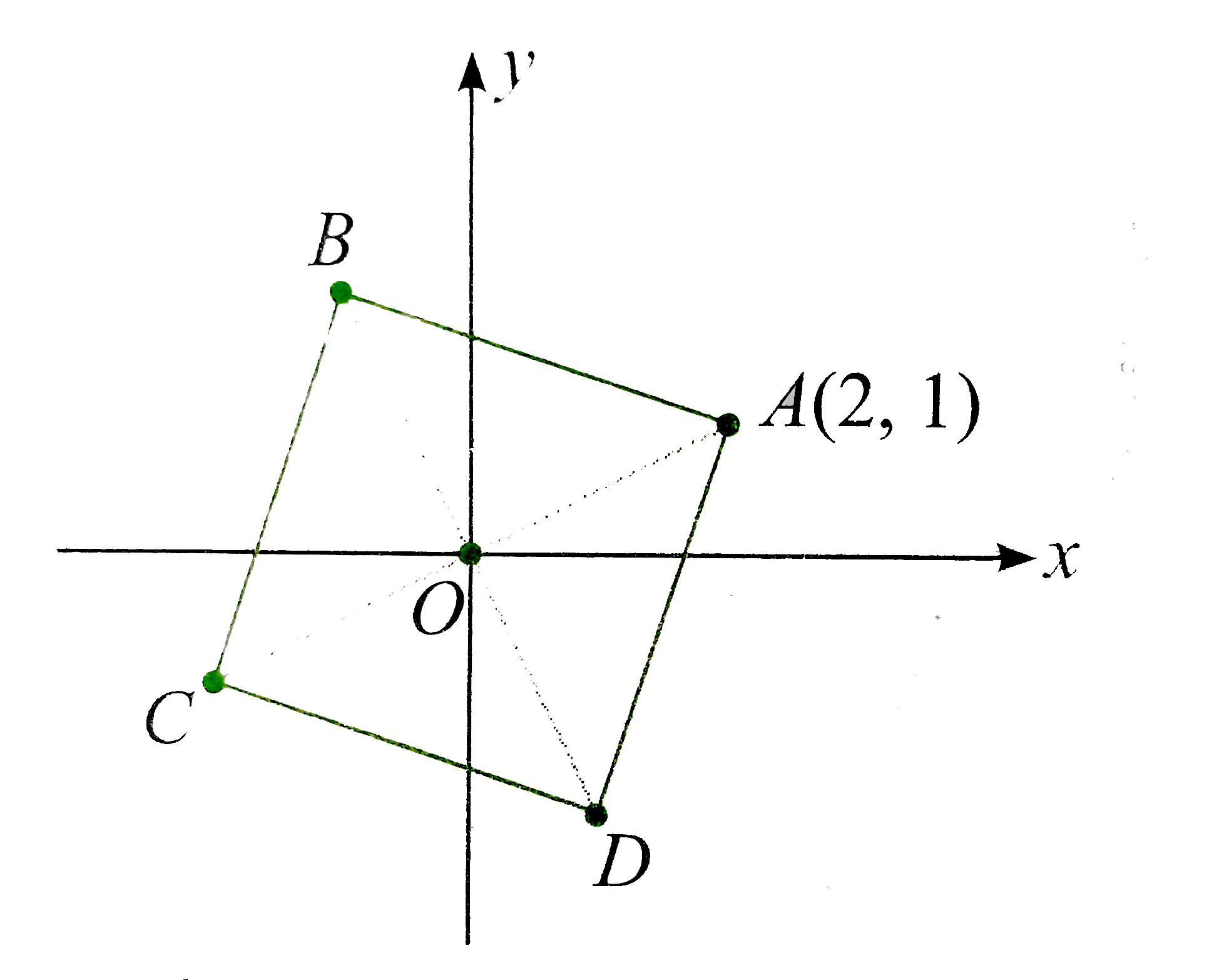
ABCD is square having centre at origin.
Clearly, C≡(−2,−1)
AO=√5
Slope of AO=1−02−0=12
∴ Slope of BD=−2
⇒−2=tanθ
∴ cosθ=−1√5 and sinθ=2√5
Since B and D are on BD at a distance √5 from O, their coordinates (in some order) will be
(0±√5cosθ,0±√5sinθ)
(0−+1,0±2)
or (-1,2 and (1,-2)
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.37videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.48videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.123videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
The center of a square is at the origin and its one vertex is A(3,2). Find the coordinates of the other vertices of the square.
View SolutionThe center of a square is at the origin and its one vertex is A(2,1). Find the coordinates of the other vertices of the square.
View SolutionThe centre of a square is at the origin and one of the vertex is 1−i extremities of diagonal not passing through this vertex are
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionThe opposite vertices of a square are (2, 6) and (0, -2). Find the coordinates of the other vertices.
View SolutionThe two opposite vertices of a square are (1, 2) and (3, 2). Find the coordinates of the other two vertices.
View SolutionThe co-ordinates of the extremities of one diagonal of a square are (1,1) and (1,−1) Find the co-ordinates of its other vertices and the equation of the other diagonal
View SolutionA(3,2)andB(−2,1) are two vertices of a triangle ABC whose centroid G has the coordinates (53,−13). Find the coordinates of the third vertex C of the triangle.
View SolutionIf one side of the square is 2x−y+6=0, then one of the vertices is (2,1) . Find the other sides of the square.
View SolutionIf one side of the square is 2x−y+6=0, then one of the vertices is (2,1) . Find the other sides of the square.
View Solution


