Question

Line $L$
has intercepts $aandb$
on the coordinate axes. When the axes are rotated through a given angle
keeping the origin fixed, the same line $L$
has intercepts $pandq\stackrel{.}{}$
Then
$a^2+b^2=p^2+q^2$

$\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{p^2}+\frac{1}{q^2}$

$a^2+p^2=b^2+q^2$
(d) $\frac{1}{a^2}+\frac{1}{p^2}=\frac{1}{b^2}+\frac{1}{q^2}$

Options

A. (a) `a^2+b^2=p^2+q^2`
B. (b) `1/(a^2)+1/(b^2)=1/(p^2)+1/(q^2)`
C. (c) `a^2+p^2=b^2+q^2`
D. (d) `1/(a^2)+1/(p^2)=1/(b^2)+1/(q^2)`

Explanation

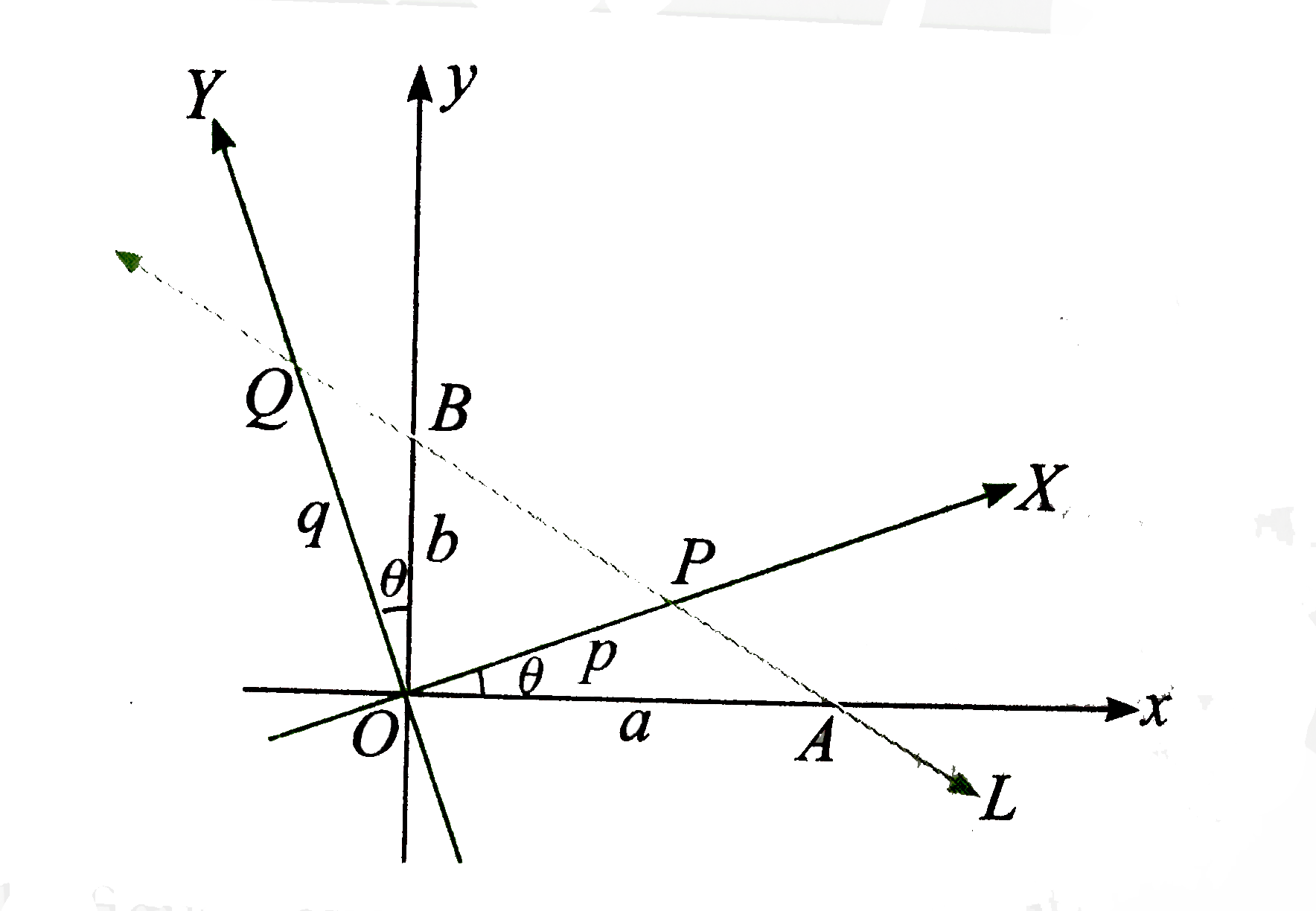
As shown in the figure, axes are rotated by an angle `theta` about origin in anticlockwise direction.
Line L has intercepts a and b on original axes and intercepts p and q on rotated axes.
Equation of line L w.r.t. original axes is
`(x)/(a) + (y)/(b)-1= 0 " " (1)`
Equation of line L w.r.t. rotated axes is
`(x)/(p) + (y)/(q)-1= 0 " " (2)`
Since origin and line L are not changing their positions, distance of line from origin remains the same even though the axes are rotated.
So, comaring distances of lines given by equations (1) and (2) from origin, we get
`(|(0)/(a) + (0)/(b)-1|)/(sqrt((1)/(a^(2))+ (1)/(b^(2)))) = (|(0)/(p) + (0)/(q)-1|)/(sqrt((1)/(p^(2))+ (1)/(q^(2))))`
`rArr (1)/(a^(2)) + (1)/(b^(2)) = (1)/(p^(2)) + (1)/(q^(2))`