ABCD is a square whose vertices are A(0,0),B(2,0),C(2,2), and D(0,2) . The square is rotated in the XY−plane through an angle 300 in the anticlockwise sense about an axis passing though A perpendicular to the XY−plane . Find the equation of the diagonal BD of this rotated square.
We have
B≡(2cos30∘,2sin30∘)=(√3,1)
D≡(−2sin30∘,2cos30∘)=(−1,√3)
Hence, the equation of BD is
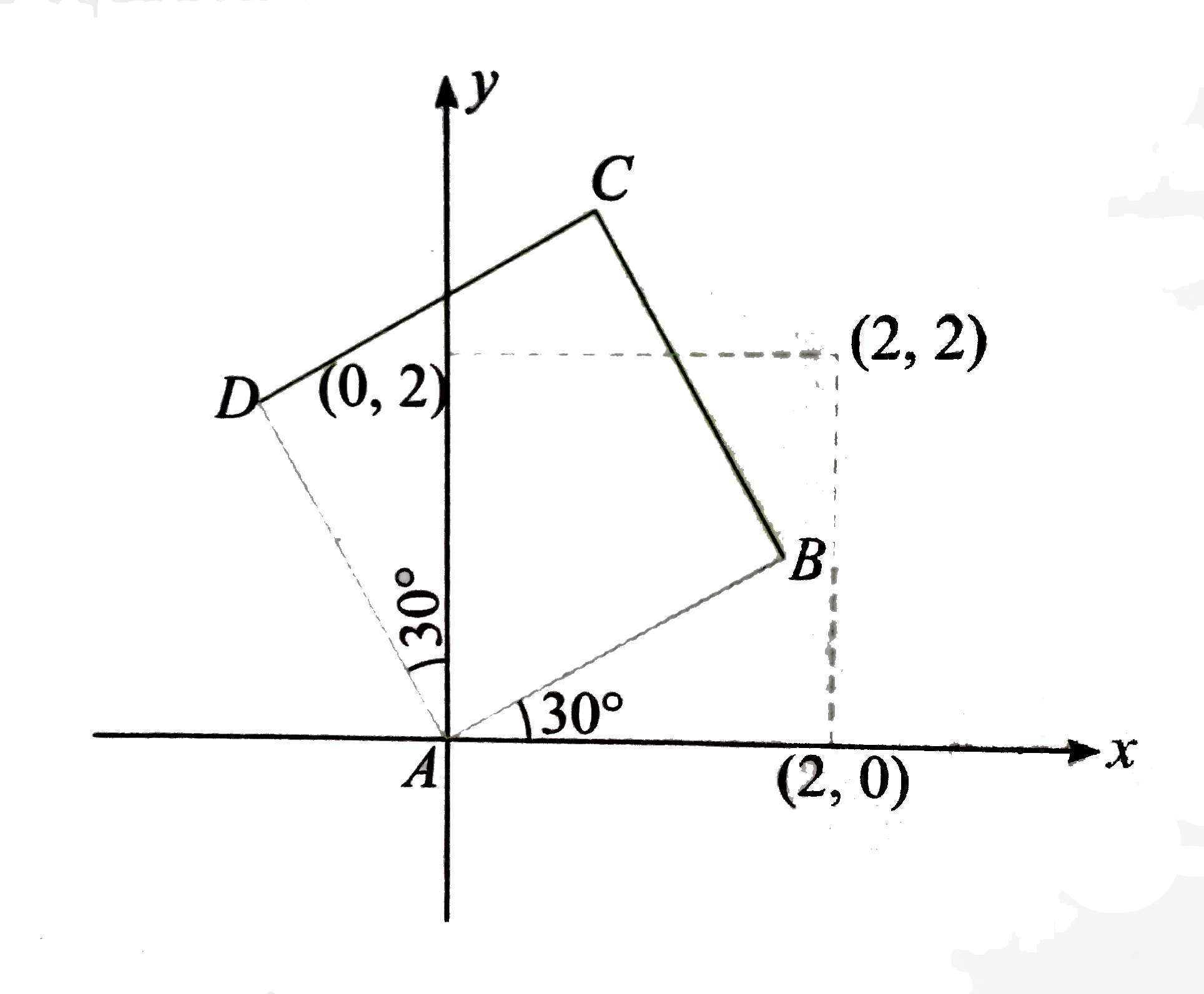
y−1=√3−1−(√3+1)(x−√3)
=(√3−2)(x−√3)
i.e., (2−√3)x+y=2√3−2
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE
12 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.1
23 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
Show that the points A(2,1),B(0,3),C(−2,1)andD(0,−1) are the vertices of a square.
View SolutionThe line segment joining A(3,0)andB(5,2) is rotated about A in the anticlockwise direction through an angle of 450 so that B goes to C. If D is the reflection of C in y-axis, find the coordinates of D.
View SolutionThe area (in square units ) of the triangle formed by y-axis , the straight line L passing through (1,1) and (2,0) and the straight line perpendicular to the line L and passing through (1/2, 0) , is
View SolutionFind the equation of a straight line passing through the point of intersection of x+2y+3=0 and 3x+4y+7=0 and perpendicular to the straight line x−y+9=0.
View SolutionThe line PQ whose equation is x−y=2 cuts the x-axis at P,andQ is (4,2). The line PQ is rotated about P through 450 in the anticlockwise direction. The equation of the line PQ in the new position is y=−√2 (b) y=2 x=2 (d) x=−2
View SolutionABC is an equilateral triangle with A(0,0) and B(a,0) , (a>0). L, M and N are the foot of the perpendiculars drawn from a point P to the side AB,BC,andCA , respectively. If P lies inside the triangle and satisfies the condition PL2=PM.PN, then find the locus of P.
View SolutionABC is an equilateral triangle with A(0,0) and B(a,0) , (a>0). L, M and N are the foot of the perpendiculars drawn from a point P to the side AB,BC,andCA , respectively. If P lies inside the triangle and satisfies the condition PL2=PM.PN, then find the locus of P.
View SolutionFind the equation of the circle passing through the point of intersection of the lines x+3y=0 and 2x−7y=0 and whose centre is the point of intersection of the lines x+y+1=0 and x−2y+4=0.
View SolutionThe medians AD and BE of a triangle with vertices A(0,b), B(0,0) and C(a,0) are perpendicular to each other, if a=b2 b. b=a2 c. ab=1 d. a=±√2b
View SolutionDetermine the point in XY−plane whcih is equidistant from three points A(2,0,3),B(0,3,2)andC(0,0,1).
View Solution
