Solve (x−3)(x+5)(x−7)|x−4|(x+6)≤0
Video Solution
Text Solution
The correct Answer is:x∈(−6,−5]∪[3,4)∪(4,7]
Sing of expression does not change while crossing x=4 as we have |x-4|.
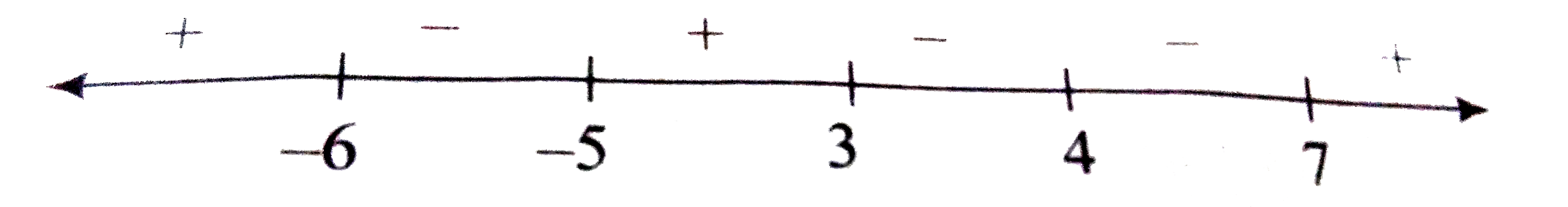 From the sign scheme ,we have x∈(−6,−5]∪[3,4)∪(4,7]
From the sign scheme ,we have x∈(−6,−5]∪[3,4)∪(4,7]
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Concept Application Exercise 1.411videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Concept Application Exercise 1.512videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Concept Application Exercise 1.28videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
- BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type6videos
SOLUTIONS AND PROPERTIES OF TRIANGLE
Similar Questions
Solve : 5x=7x−4
View SolutionSolve: 3x+52x+7=4
View SolutionSolve (2x+3)(4−3x)3(x−4)(x−2)2x5≤0
View SolutionSolve (2x+3)(4−3x)3(x−4)(x−2)2x5≤0
View SolutionLet 'a' be an integer. If there are 10 inegers satisfying the (x−a)2(x−2a)(x−3a)(x−4a)≤0 then
View SolutionSolve (x−5)2(x+2)3(x−4)(x−3)4≤0
View SolutionSolve for x: x−4x−5+x−6x−7=103;x≠5,7
View SolutionSolve 4x+3<6x+7.
View SolutionSolve 4x+3<6x+7.
View SolutionSolve: (4+x)(5−x)(2+x)(7−x)=1
View Solution


