The perpendicular distance of a corner of uni cube from a diagonal not passing through it is
The correct Answer is:√23
To find the perpendicular distance of a corner of a unit cube from a diagonal not passing through it, we can follow these steps:
1. Understanding the Unit Cube:
- A unit cube has vertices at coordinates (0,0,0), (1,0,0), (0,1,0), (0,0,1), (1,1,0), (1,0,1), (0,1,1), and (1,1,1).
- Let's denote the corner point P as (1,1,1).
2. Identifying the Diagonal:
- We need to consider a diagonal that does not pass through point P. A suitable diagonal is from (0,0,0) to (1,1,1). However, we can consider the diagonal from (0,0,0) to (1,1,0) which lies in the plane z=0.
3. Position Vectors:
- The position vector of point P is →OP=^i+^j+^k.
- The position vector of point O (the origin) is →O=0^i+0^j+0^k.
4. Finding the Unit Vector of the Diagonal:
- The diagonal vector →d from (0,0,0) to (1,1,0) is →d=^i+^j.
- The magnitude of →d is |→d|=√12+12=√2.
- The unit vector ^d in the direction of the diagonal is given by:
^d=→d|→d|=^i+^j√2.
5. Calculating the Projection:
- The projection of →OP onto ^d is given by:
Projection=→OP⋅^d=(^i+^j+^k)⋅(^i+^j√2).
- Calculating the dot product:
→OP⋅^d=1√2(1+1+0)=2√2=√2.
6. Finding the Length of the Perpendicular:
- The length of the perpendicular from point P to the diagonal can be found using the Pythagorean theorem:
d=√|→OP|2−(Projection)2.
- Here, |→OP|=√12+12+12=√3.
- Therefore, we have:
d=√3−2=√1=1.
Final Answer:
The perpendicular distance of the corner of the unit cube from the diagonal not passing through it is √23.
- A unit cube has vertices at coordinates (0,0,0), (1,0,0), (0,1,0), (0,0,1), (1,1,0), (1,0,1), (0,1,1), and (1,1,1).
- Let's denote the corner point P as (1,1,1).
- We need to consider a diagonal that does not pass through point P. A suitable diagonal is from (0,0,0) to (1,1,1). However, we can consider the diagonal from (0,0,0) to (1,1,0) which lies in the plane z=0.
- The position vector of point P is →OP=^i+^j+^k.
- The position vector of point O (the origin) is →O=0^i+0^j+0^k.
- The diagonal vector →d from (0,0,0) to (1,1,0) is →d=^i+^j.
- The magnitude of →d is |→d|=√12+12=√2.
- The unit vector ^d in the direction of the diagonal is given by:
^d=→d|→d|=^i+^j√2.
- The projection of →OP onto ^d is given by:
Projection=→OP⋅^d=(^i+^j+^k)⋅(^i+^j√2).
- Calculating the dot product:
→OP⋅^d=1√2(1+1+0)=2√2=√2.
- The length of the perpendicular from point P to the diagonal can be found using the Pythagorean theorem:
d=√|→OP|2−(Projection)2.
- Here, |→OP|=√12+12+12=√3.
- Therefore, we have:
d=√3−2=√1=1.
The perpendicular distance of the corner of the unit cube from the diagonal not passing through it is √23.
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - SINGLE CORRECT ANSWER TYPE
86 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CORRECT ANSWER TYPE
17 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - CONCEPT APPLICATION EXERCISE 3.4
5 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
Similar Questions
Find the perpendicular distance of an angular point of a cube from a diagona which does not pass through that angular point. (a) 1√3 (b) 23 (c) √23 (d) √32
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionFind the equation of a curve passing through the point (1.1) if the perpendicular distance of the origin from the normal at any point P(x, y) of the curve is equal to the distance of P from the x-axis.
View SolutionThe perpendicular distance from the origin to the plane through the point (2,3,-1) and perpendicular to the vector 3ˆi−4ˆj+7ˆk is
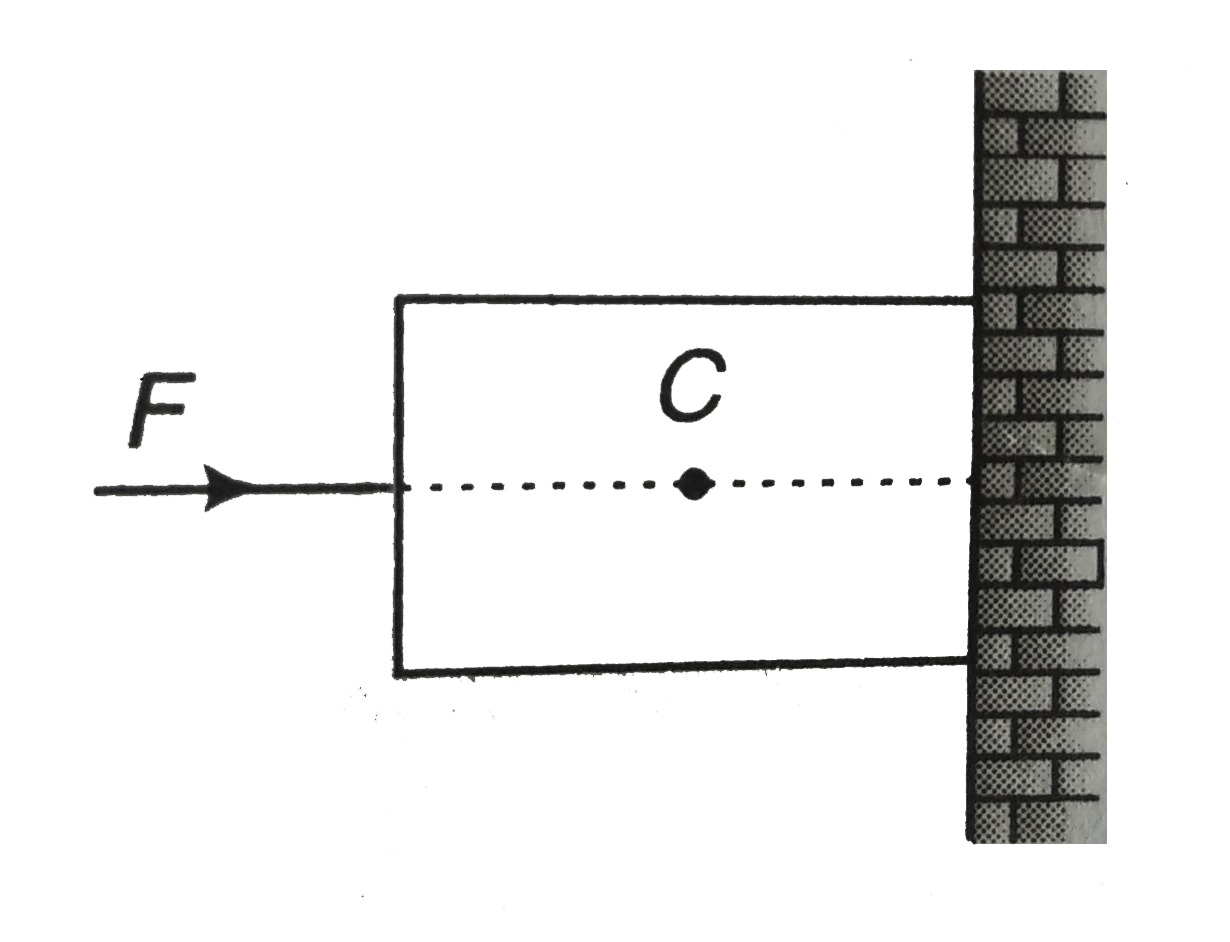
View SolutionA cube of mass 2kg is help stationary against a rough wall by a force F=40N passing through center C . Find perpendicular distance of normal reaction between wall and cube from point C. Side of the cube is 20cmTakeg=10m/s2.
View SolutionA field in the form of a parallelogram has one of its diagonals 42 m long the perpendicular distance of this diagonal from either of the outlying vertices is 10.8 m. Find the area of the field.
View SolutionA field in the form of a parallelogram has one of its diagonals 42 m long the perpendicular distance of this diagonal from either of the outlying vertices is 10.8 m. Find the area of the field.
View SolutionThe length of each side of a cubical closed surface is L metre. If charge 48C is situated at one of the corners of the cube, Find the flux passing through the cube. (In Volt-metre)
View SolutionProve that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
View Solution
