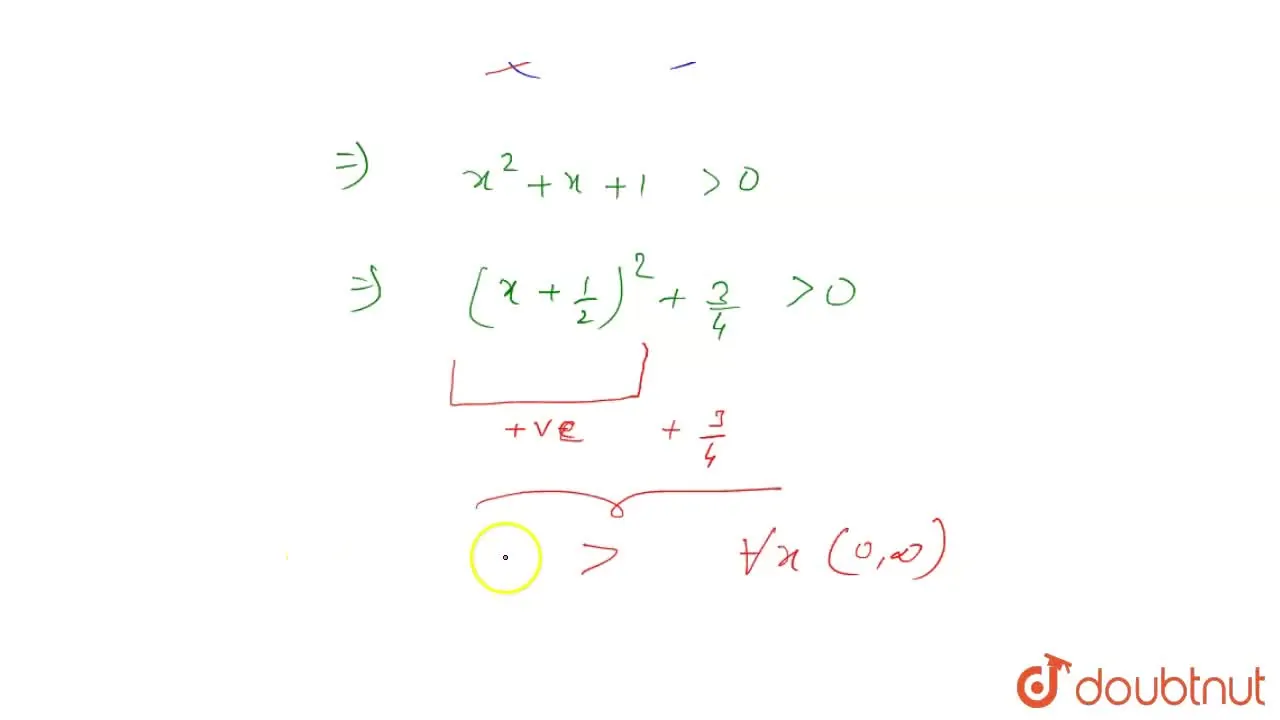Prove that 2log21/4x−3log27(x2+1)3−2x74log49x−x−1>0,∀x∈(0,∞).
Video Solution
Text Solution
2log21/4x−3log27(x2+1)3−2x74log49x−x−1
=2log2x4−3log3(x2+1)−2x7log7x2−x−1
x2−(x2+2x+1)x2−x−1
=x2+x+1
(x+12)2+34>0,∀x∈R
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - ILLUSTRATION 1.421videos
LOGARITHM AND ITS PROPERTIES
- BOOK - CENGAGE ENGLISHCHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - ILLUSTRATION 1.431videos
LOGARITHM AND ITS PROPERTIES
- BOOK - CENGAGE ENGLISHCHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - ILLUSTRATION 1.401videos
LOGARITHM AND ITS PROPERTIES
- BOOK - CENGAGE ENGLISHCHAPTER - LOGARITHM AND ITS APPLICATIONS EXERCISE - Subjective Type9videos
LOGARITHM AND ITS APPLICATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
Similar Questions
Prove that 2(log)214x−3(log)27(x2+1)3−2x74(log)49x−x−1>0
View SolutionLet y=2log21/4x−3log27(x2+1)3−2x74log49x−x−1 and dydx=ax+b, the ordered pair (a, b) is
View SolutionThe value of 2log2142−3log27125−4(74log492)−3 is
View SolutionLet y=2(log)214x−3(log)27(x2+1)3−2x74(log)49x−x−1anddydx=ax+b, then the value of a+b is_______.
View SolutionSolve the equation 2xlog34+3logx4=27
View SolutionSolve log4(x−1)=log2(x−3).
View SolutionSolve 14xlog2√x=(2⋅xlog2x)14.
View SolutionSolve 4log9x−6xlog92+2log327=0.
View SolutionSolve the equation log2(3−x)−log2⎛⎝sin3π45−x⎞⎠=12+log2(x+7)
View SolutionSolve : log1−2x(6x2−5x+1)−log1−3x(4x2−4x+1)=2
View Solution