Question

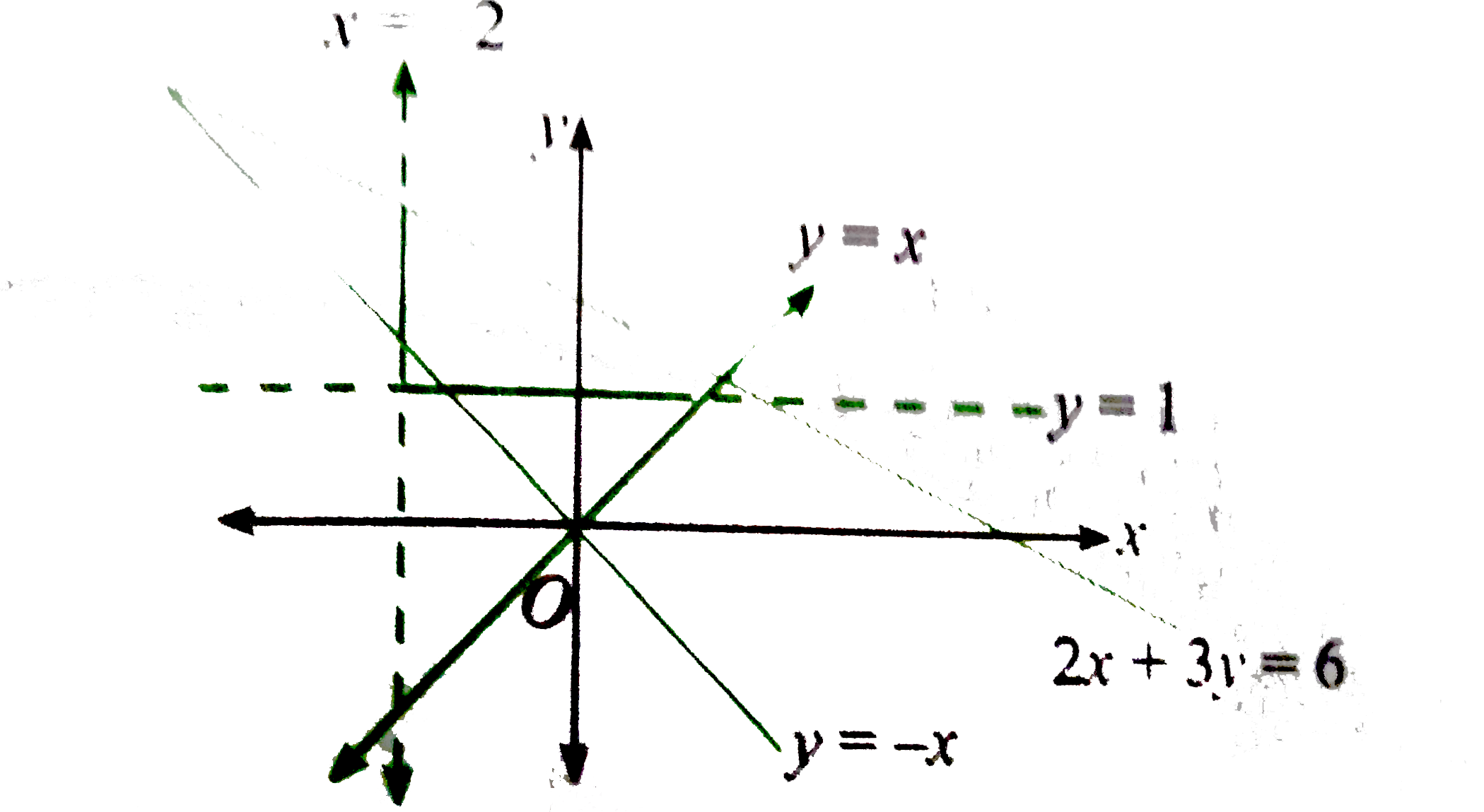
The combined equation of three sides of a triangle is $(x^2-y^2)(2x+3y-6)=0$. If $(-2,a)$ is an interior point and $(b,1)$ is an exterior point of the triangle, then

Options

A. `2ltalt10//3`
B. `-2ltalt10//3`
C. `-1ltblt9//2`
D. `-1ltblt1`

Answer

1,4

Explanation

To solve the problem step-by-step, we will analyze the combined equation of the triangle's sides and determine the interior and exterior points based on the given coordinates.

Step 1: Understand the Combined Equation
The combined equation of the triangle is given as:
\( (x^2 - y^2)(2x + 3y - 6) = 0 \)
This means that the triangle is formed by the lines represented by \(x^2 - y^2 = 0\) and \(2x + 3y - 6 = 0\).

Step 2: Factor the First Part
The equation \(x^2 - y^2 = 0\) can be factored as:
\( (x - y)(x + y) = 0 \)
This gives us two lines:
1. \(x - y = 0\) or \(y = x\)
2. \(x + y = 0\) or \(y = -x\)

Step 3: Analyze the Second Part
The second part of the equation \(2x + 3y - 6 = 0\) can be rearranged to find the slope-intercept form:
\( 3y = -2x + 6 \implies y = -\frac{2}{3}x + 2 \)
This line has a slope of \(-\frac{2}{3}\) and a y-intercept of \(2\).

Step 4: Identify the Triangle's Vertices
To find the vertices of the triangle, we need to find the intersection points of the lines:
1. Intersection of \(y = x\) and \(y = -\frac{2}{3}x + 2\):
\( x = -\frac{2}{3}x + 2 \implies \frac{5}{3}x = 2 \implies x = \frac{6}{5}, \quad y = \frac{6}{5} \)
So one vertex is \(\left(\frac{6}{5}, \frac{6}{5}\right)\).

2. Intersection of \(y = -x\) and \(y = -\frac{2}{3}x + 2\):
\( -x = -\frac{2}{3}x + 2 \implies \frac{1}{3}x = 2 \implies x = 6, \quad y = -6 \)
So another vertex is \((6, -6)\).

3. Intersection of \(y = x\) and \(y = -x\):
\( x = -x \implies 2x = 0 \implies x = 0, \quad y = 0 \)
So the third vertex is \((0, 0)\).

Step 5: Determine the Interior Point
The interior point given is \((-2, a)\). To find the value of \(a\), we need to check if this point lies inside the triangle formed by the vertices \(\left(\frac{6}{5}, \frac{6}{5}\right)\), \((6, -6)\), and \((0, 0)\).

Step 6: Check the Point
To check if \((-2, a)\) is an interior point, we substitute \(x = -2\) into the line equation \(2x + 3y - 6 = 0\):
\( 2(-2) + 3a - 6 = 0 \implies -4 + 3a - 6 = 0 \implies 3a = 10 \implies a = \frac{10}{3} \)

Step 7: Determine the Exterior Point
The exterior point given is \((b, 1)\). We substitute \(y = 1\) into the line equation \(2x + 3y - 6 = 0\):
\( 2x + 3(1) - 6 = 0 \implies 2x + 3 - 6 = 0 \implies 2x - 3 = 0 \implies x = \frac{3}{2} \)
Thus, the point \((b, 1)\) must satisfy \(b > \frac{3}{2}\) or \(b < -2\) to be outside the triangle.

Conclusion
The values we found are:
- For the interior point \((-2, a)\), \(a = \frac{10}{3}\).
- For the exterior point \((b, 1)\), \(b\) must be greater than \(\frac{3}{2}\) or less than \(-2\).