In a ABC,A≡(α,β),B≡(1,2),C≡(2,3), point A lies on the line y=2x+3, where α,β are integers, and the area of the triangle is S such that [S]=2 where [ .] denotes the greatest integer function. Then the possible coordinates of A can be (−7,−11) (−6,−9) (2,7) (3,9)
(−7,−11)
(−6,−9)
(2,7)
(3,9)
The point A(α,β) lies on y=2x+3.
Hence,
β=2α+3
A=(α,2α+3)
Area of ΔABC is ∣∣
∣∣12∣∣
∣∣α2α+31121231∣∣
∣∣∣∣
∣∣
=∣∣∣12[α(2−3)+(2α+3)(2−1)+1(3−4)]∣∣∣
=12|−α+2α+3−1|=12|α+2|=S
[S]=2or2≤S<3
therfore2≤12|α+2|<3
4≤|α+2|<6
|α+2|≤6
or −6≤α+2≤6
or −8≤α≤4
and |α+2|≥4
i.e., α+2≥4orα+2≤−4
i.e., α≥2orα≤−6
From (1) and (2) , we get
−8<α<−6or2≤α<4
or α=−7,−6,2,3
The possible coordiantes of A are (−7,−11),(−6,−9),(2,7) and (3,9). 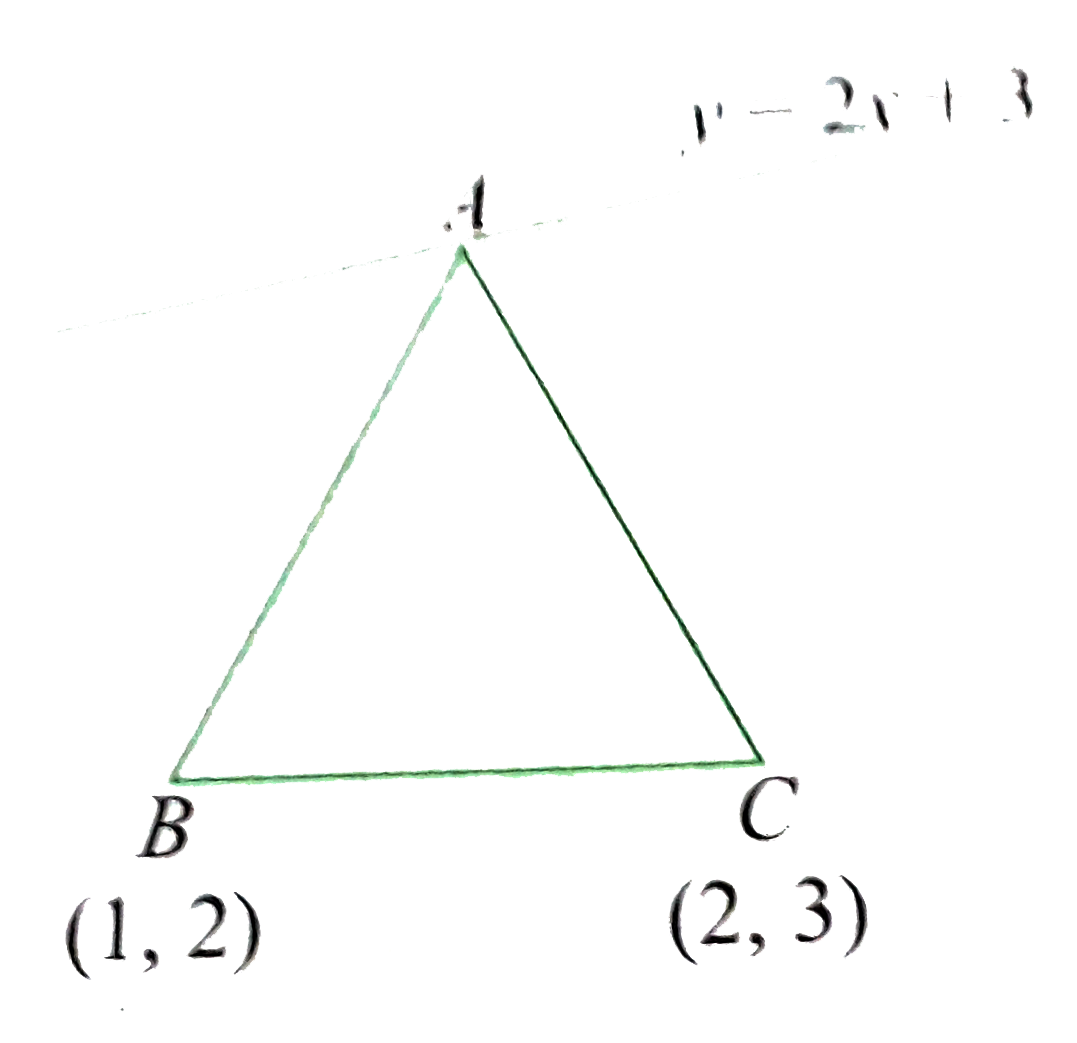
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
In a ABC,A≡(α,β),B≡(1,2),C≡(2,3), point A lies on the line y=2x+3, where α,β are integers, and the area of the triangle is S such that [S]=2 where [ .] denotes the greatest integer function. Then the possible coordinates of A can be (−7,−11) (−6,−9) (2,7) (3,9)
View Solutionif α is a real root of 2x3−3x2+6x+6=0, then find [α] where [] denotes the greatest integer function.
View SolutionArea of the region bounded by [x]2=[y]2,ifx∈[1,5], where [ ] denotes the greatest integer function is:
View SolutionIn a triangle ABC,A=(α,β)B=(2,3),andC=(1,3). Point A lies on line y=2x+3, where α∈I. The area of ABC, , is such that [Δ]=5 . The possible coordinates of A are (where [.] represents greatest integer function). (a)(2,3) (b) (5,13) (−5,−7) (d) (−3,−5)
View SolutionIf [f(√32)] is [.] denotes the greatest integer function) 4 (b) 5 (c) 6 (d) −7
View SolutionThe area enclosed by the curve
[x+3y]=[x−2] where x∈[3,4] is :
(where[.] denotes greatest integer function)
View SolutionThe period of the function f(x)=[6x+7]+cosπx−6x, where [.] denotes the greatest integer function is: (a)3 (b) 2π (c) 2 (d) none of these
View SolutionIf [x]2−5[x]+6=0, where [.] denotes the greatest integer function, then x∈[3,4] (b) x∈(2,3] (c) x∈[2,3] (d) x∈[2,4)
View SolutionIf the least bounded by the curves y=x2 and y=λx+12 is equal to αβ, then [α20β] is equal to ________(where [.] denotes the greatest integer function)
View SolutionIf complete solution set of e−x≤4−x is [α,β] then [α]+[β] is equal to : (where [.] denotes greatest integer function )
View Solution
