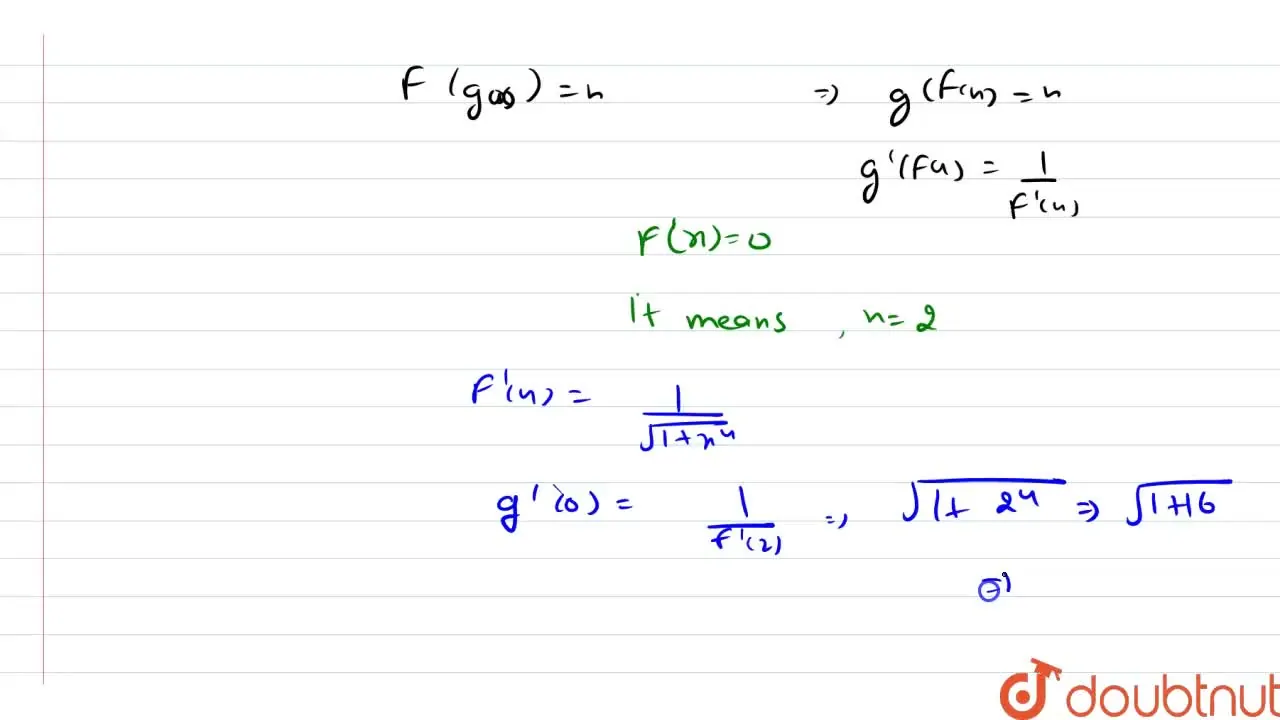Let f(x)=∫x2dt√1+t4andg(x) be the inverse of f(x) . Then the value of g'(0)
Step by step video & image solution for Let f(x)=int_2^x(dt)/(sqrt(1+t^4))a n dg(x) be the inverse of f(x) . Then the value of g'(0) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Let f(x)=∫x0dt√1+t3 and g(x) be the inverse of f(x). Then the value of 4g''(x)g(x)2 is________.
View SolutionLet f(x)=∫x2dt√1+t4andg be the inverse of f. Then, the value of g'(0) is
View SolutionIf f(x)=∫x2dt1+t4, then
View SolutionLet f(x)=∫x2f(t2−3t+4)dt. Then
View SolutionLet f(x)=−4.√e1−x+1+x+x22+x33. If g(x) is inverse of f(x) then the value of 1g′(−76) is
View SolutionLet f(x)=∫x−2|t+1|dt, then
View SolutionLet f(x)=∫x13t1+t2dt, where x>0, Then
View SolutionIf f(x)=∫g(x)0dt√1+t3,g(x)=∫cosx0(1+sint)2dt, then the value of f'(π2) is equal to:
View SolutionIf f(x)=∫g(x)0dt√1+t3,g(x)=∫cosx0(1+sint)2dt, then the value of f'(π2) is equal to:
View Solutionf(x)=∫x0f(t)dt=x+∫1xtf(t)dt, then the value of f(1) is
View Solution