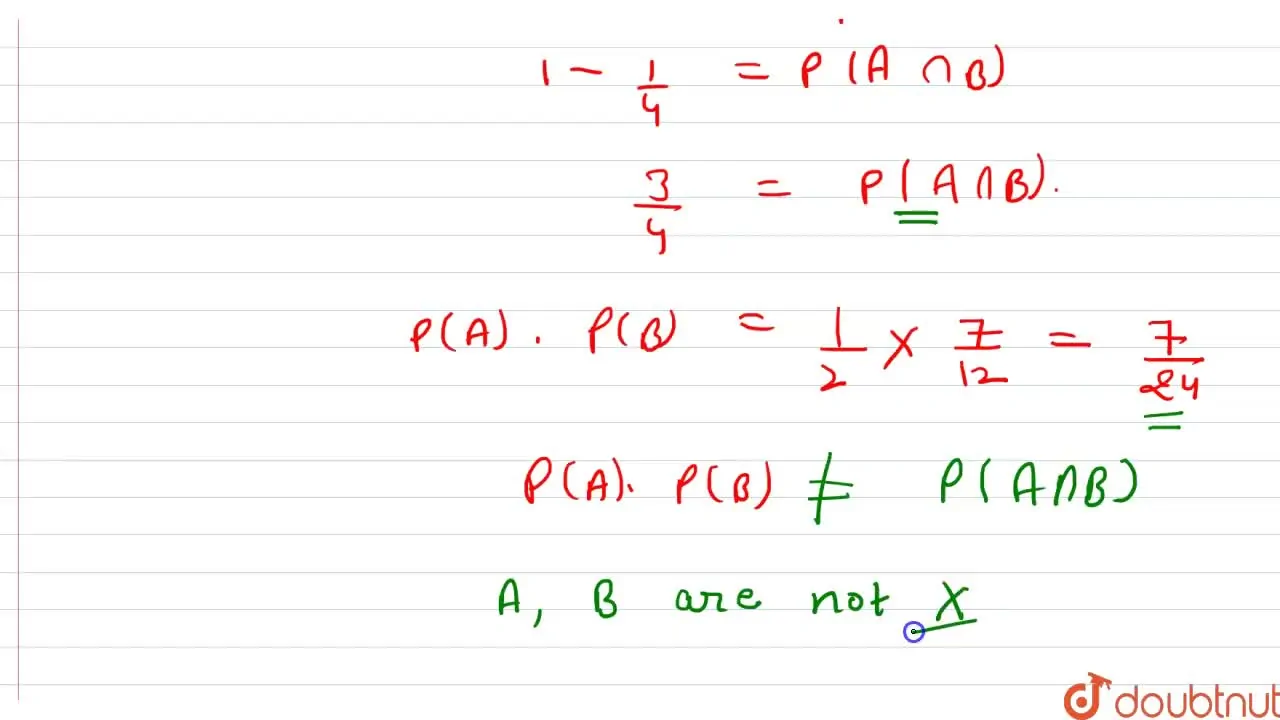Events AandB are such that P(A)=1/2,P(B)=7/12,andP(¬Aor¬B)=1/4. State whether AandB are independents?
It is given that P(A)−12,P(B)=72,andP(not A or not B)=14
=P(A'∪B')=14
⇒P((A∩B)')=14 [∵A'∪B'=(A∩B']
⇒a−P(A∩B)=14
or P(A∩B)=34 (1)
However P(A).P(B)=12×712=724 (2)
Here, 34≠724
∴P(A∩B)≠P(A).P(B)
Therefore, A and B are not independent events.
Similar Questions
Events A and B are such that P(A)=12, P(b)=712 and P( not A or not)=14 . State whether A and B are independent?
View SolutionIf A and B are two events such that P(A)=12, P(B)=712and P(not A or not B) = 14. State whether A and B are independent?
View SolutionA and B are two events such that P(A)=35,P(B)=310 and P(A∪B)=12
Find whether A and B are independent or not.View SolutionIf A and B be two events such that P(A)=1/4, P(B)=1/3 and P(A∪B)=1/2 show that A and B are independent events.
View SolutionIf P(A)=14,P(B)=13andP(AUB)=12, prove that A and B are independent events
View Solutionif A and B be two events such that P(A)=14,P(B)=13 and P(A∪B)=12, show that A and B are independent events.
View SolutionIf A and B are events such that P(A)=12,P(B)=13andP(A∩B)=14, then find
(a) P(A/B)
(b) P(B/A)View SolutionIf A and B are events such that P(A) = 12 , P(B) = 13 and P(A ∩ B) =14 then find P(A |B)
View SolutionIf A and B are two events such that P(A)=12,P(B)=13andP(A/B)=14 then P(A∩B) is equal to
View SolutionIf A and B are two events such that P(A)=14,P(B)=12and P(A∩B)=18 , find P (not A and not B).
View Solution