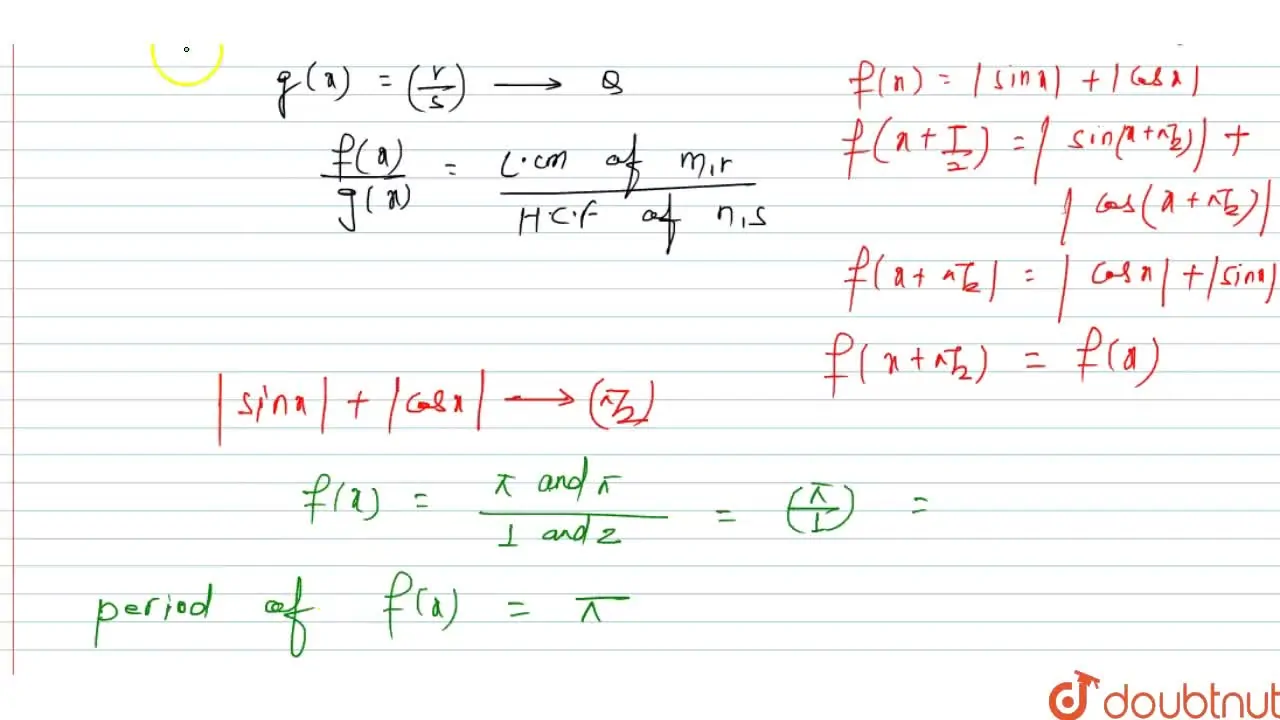Find the period (if periodic) of the following function ([.] denotes the greatest integer functions): f(x)=|sinx+cosx||sinx|+|cosx|
Step by step video & image solution for Find the period (if periodic) of the following function ([.] denotes the greatest integer functions): f(x)=(|sinx+cosx|)/(|sinx|+|cosx|) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Find the period (if periodic) of the following function ([.] denotes the greatest integer functions): f(x)=tanπ2[x]
View SolutionFind the period (if periodic) of the following function ([.] denotes the greatest integer functions): f(x)=x−[x−b],b∈R
View SolutionFind the periods (if periodic) of the following functions, where [.] denotes the greatest integer function
cosec(3x−5)View SolutionFind the periods (if periodic) of the following functions, where [.] denotes the greatest integer function
f(x)=|sinx+cosx||sinx|+|cosx|View SolutionWhich of the following function are not periodic (where [.] denotes greatest integer function:
f(x)=x+sinxView SolutionWhich of the following function are not periodic (where [.] denotes greatest integer function:
f(x)=sin√xView SolutionWhich of the following function is not periodic, where [.] denotes greatest integer function
View SolutionWhich of the following function are not periodic (where [.] denotes greatest integer function:
f(x)=[sin3x]+|cos6x|View SolutionThe period of the function f(x)=Sin(x+3−[x+3])where [] denotes the greatest integer function
View SolutionThe peroid of the function f(x)=|sinx|−|cosx||sinx+cosx| is
View Solution