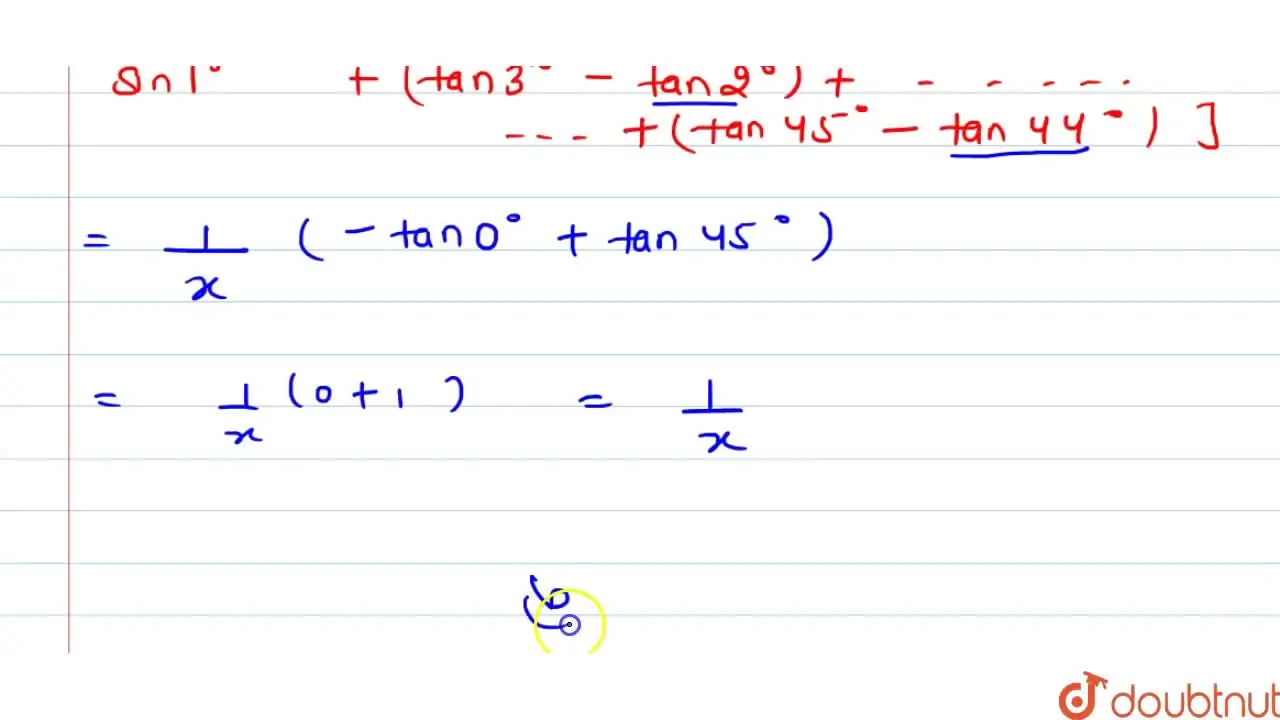Let x=sin10, then the value of the expression. 1cos00.cos10+1cos10.cos20+1cos20.cos30+1cos440.cos450 is equal to (a) x (b) 1x (c) √2x (d) x√2
1sin1[sin(1−0)cos0cos1+sin(2−1)cos2cos2+....+sin(45−44)cos44cos45]
1sin1[tan1−tan0+tan2−tan2+tan3−tan2+...+tan45−tan44]
1sin1⋅[1−0]
1sin1
1x.
Related Playlists
Similar Questions
Let x=sin1∘ then find the value of the expression 1cos0∘cos1∘+1cos1∘cos2∘+....+1cos44∘cos45∘
View SolutionValue of (1−cos610cos10)⋅(1−cos620cos20)⋅(1−cos630cos30)..........⋅(1−cos1190cos590) (a)−1 (b) 1 (c) 2 (d) −2
View Solution(lim)x→∞sin4x−sin2x+1cos4x−cos2x+1 is equal to (a) 0 (b) 1 (c) 13 (d) 12
View Solutioncos350+cos850+cos1550 a. a. 0 b. 1√2 c. 1√3 d. cos2750
View Solutionthe value of cos(cos−1x+sin−1(x−2)) is equal to (A) 0 (B) 1 (C) -1 (D) √1−x2.√x2−4x+3+x(x−2)
View SolutionThe value of expression 2(sin10+sin20+sin30+...+sin890)2(cos10+cos20++cos440)+1 (a)√2 (b) 1√2 (c) 12 (d) 0
View SolutionIf x∈[−1,0], then find the value of cos−1(2x2−1)−2sin−1x
View SolutionIf x∈[−1,0) then find the value of cos−1(2x2−1)−2sin−1x
View SolutionIf cos(sin−1(2√5)+cos−1x) = 0, then x is equal to
A) 1√5
B) (−2√5)
C) (2√5)
D) 1View Solutionlimx→01−cosxx√x2
View Solution