Let ABC be an acute angled triangle whose orthocentre is at H. If altitude from A is produced to meet the circumcircle of triangle ABC at D , then prove HD=4RcosBcosC
To prove that HD=4RcosBcosC for triangle ABC with orthocenter H and point D where the altitude from A meets the circumcircle, we can follow these steps:
Step 1: Understand the Geometry
Let ABC be an acute-angled triangle with vertices A, B, and C. The orthocenter H is the intersection of the altitudes of the triangle. The point D is where the altitude from A meets the circumcircle of triangle ABC.
Step 2: Draw the Diagram
Draw triangle ABC with the circumcircle. Mark the orthocenter H and the foot of the altitude from A to BC as N. Extend the altitude from A to meet the circumcircle at point D.
Step 3: Analyze Angles
In triangle BHD:
- ∠BNH=90∘ (since N is the foot of the altitude from A).
- ∠BND=∠BNH=90∘.
- ∠BHC=180∘−∠A (since H is the orthocenter).
Step 4: Use Triangle Congruence
Triangles BHN and BDN are similar:
- ∠BNH=∠BND=90∘.
- ∠BHN=∠BDN (common angle).
- Side BN is common.
Thus, by the Angle-Angle (AA) criterion, triangles BHN and BDN are congruent.
Step 5: Establish Relationships
From the congruence, we have:
HN=ND
Let HN=x. Therefore, ND=x as well.
Step 6: Relate HN to R
Using the formula for the length of the altitude in terms of the circumradius R:
HN=2RcosBcosC
Thus, we can write:
ND=2RcosBcosC
Step 7: Find HD
Since HD=HN+ND:
HD=HN+ND=2RcosBcosC+2RcosBcosC=4RcosBcosC
Conclusion
Thus, we have proven that:
HD=4RcosBcosC
Let ABC be an acute-angled triangle with vertices A, B, and C. The orthocenter H is the intersection of the altitudes of the triangle. The point D is where the altitude from A meets the circumcircle of triangle ABC.
Draw triangle ABC with the circumcircle. Mark the orthocenter H and the foot of the altitude from A to BC as N. Extend the altitude from A to meet the circumcircle at point D.
In triangle BHD:
- ∠BNH=90∘ (since N is the foot of the altitude from A).
- ∠BND=∠BNH=90∘.
- ∠BHC=180∘−∠A (since H is the orthocenter).
Triangles BHN and BDN are similar:
- ∠BNH=∠BND=90∘.
- ∠BHN=∠BDN (common angle).
- Side BN is common.
From the congruence, we have:
HN=ND
Let HN=x. Therefore, ND=x as well.
Using the formula for the length of the altitude in terms of the circumradius R:
HN=2RcosBcosC
Thus, we can write:
ND=2RcosBcosC
Since HD=HN+ND:
HD=HN+ND=2RcosBcosC+2RcosBcosC=4RcosBcosC
Thus, we have proven that:
HD=4RcosBcosC
Topper's Solved these Questions
Similar Questions
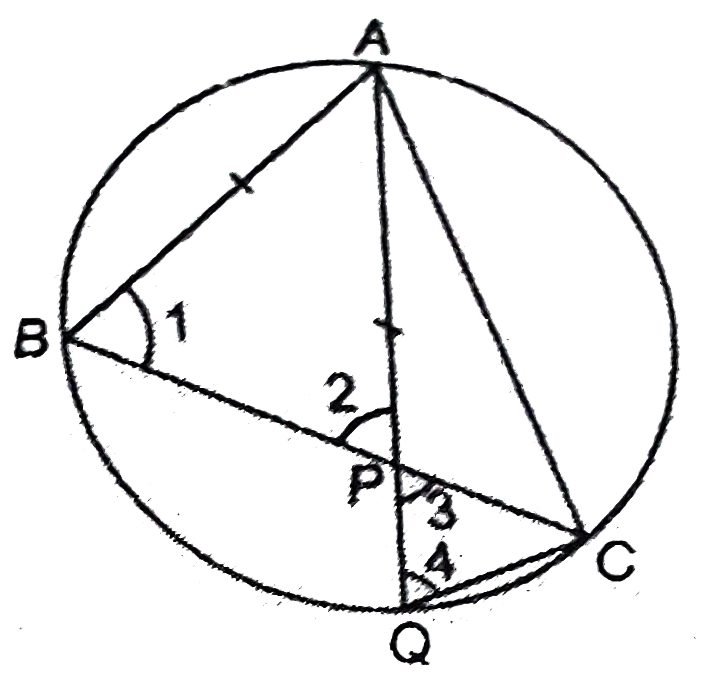
In given figure , ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
View SolutionABC is an acute angled triangle with circumcenter O and orthocentre H. If AO=AH, then find the angle A.
View SolutionABC is an acute angled triangle with circumcenter O and orthocentre H. If AO=AH, then find the angle A.
View SolutionABC is an acute angled triangle with circumcenter O and orthocentre H. If AO=AH, then find the angle A.
View SolutionIn an acute-angled triangle ABC, tanA+tanB+tanC
View SolutionLet ABC be a triangle and O be its orthocentre .If R and R1 are the circum-radii of triangle ABC and AOB , then
View SolutionIn an acute angled △ABC, the minimum value of tanAtanBtanC is
View SolutionProve that in an acute angled triangle ABC,secA+secB+secC≥6.
View SolutionA circumcircle is a circle which passes through all vertices of a triangle and an incircle is a circle which is inscribed in a triangle touching all sides of a triangle. Let ABC be a right angled triangle whose radius of circumcircle is 5 and its one side AB = 6. The radius of incircle of triangle ABC is r. The value of r is
View SolutionA circumcircle is a circle which passes through all vertices of a triangle and an incircle is a circle which is inscribed in a triangle touching all sides of a triangle. Let ABC be a right-angled triangle whose radius of the circumcircle is 5 and its one side AB = 6. The radius of incircle of triangle ABC is r. Area of Δ ABC is
View Solution
