If triangle ABC is right angled at C, then the value of sec (A+B) is
0
1
2√3
Not defined
The correct Answer is:d
To solve the problem, we need to find the value of sec(A + B) given that triangle ABC is right-angled at C.
1. Understanding the Triangle:
In triangle ABC, we know that angle C is the right angle. Therefore, angle C = 90°.
2. Sum of Angles in a Triangle:
The sum of the angles in any triangle is always 180°. Thus, we can write the equation:
A+B+C=180°
Substituting C = 90° into the equation gives:
A+B+90°=180°
3. Simplifying the Equation:
To find A + B, we can rearrange the equation:
A+B=180°−90°
This simplifies to:
A+B=90°
4. Finding sec(A + B):
We need to find sec(A + B). Since we have determined that A + B = 90°, we substitute this into the secant function:
sec(A+B)=sec(90°)
5. Understanding secant:
The secant function is defined as the reciprocal of the cosine function:
sec(x)=1cos(x)
Therefore, we can write:
sec(90°)=1cos(90°)
6. Calculating cos(90°):
We know that:
cos(90°)=0
Thus, substituting this value gives:
sec(90°)=10
7. Conclusion:
Since division by zero is undefined, we conclude that:
sec(A+B)=undefined
Final Answer:
The value of sec(A + B) is undefined.
In triangle ABC, we know that angle C is the right angle. Therefore, angle C = 90°.
The sum of the angles in any triangle is always 180°. Thus, we can write the equation:
A+B+C=180°
Substituting C = 90° into the equation gives:
A+B+90°=180°
To find A + B, we can rearrange the equation:
A+B=180°−90°
This simplifies to:
A+B=90°
We need to find sec(A + B). Since we have determined that A + B = 90°, we substitute this into the secant function:
sec(A+B)=sec(90°)
The secant function is defined as the reciprocal of the cosine function:
sec(x)=1cos(x)
Therefore, we can write:
sec(90°)=1cos(90°)
We know that:
cos(90°)=0
Thus, substituting this value gives:
sec(90°)=10
Since division by zero is undefined, we conclude that:
sec(A+B)=undefined
The value of sec(A + B) is undefined.
Topper's Solved these Questions
- SAMPLE PAPER 2019Book:X BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:18A
Explore 1 Video
- SAMPLE PAPER 2019Book:X BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:18B
Explore 1 Video
- CBSE BOARDS 2020Book:X BOARD PREVIOUS YEAR PAPER ENGLISHChapter:CBSE BOARDS 2020Exercise:QUESTION
Explore 41 Videos
- X BoardsBook:X BOARD PREVIOUS YEAR PAPER ENGLISHChapter:X BoardsExercise:All Questions
Explore 481 Videos
Similar Questions
Knowledge Check
In the figure, ABC is a right triangle. What is the value of y?
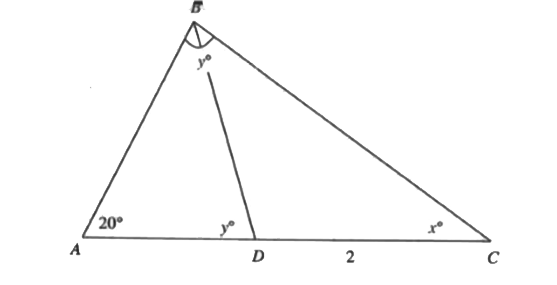 A20B30C50D90
A20B30C50D90
A triangle ABC is right angled at B, find the value of secA.sinC−tanA−tanCsinB
View SolutionThe points A(3,0) , B (a, -2) and C(4, -1) are the vertices of triangle ABC right angled at vertex A. Find the value of a.
View SolutionIf in a triangle ABC, right angled at B, s-a=3, s-c=2, then the values of a and c are respectively
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
View SolutionIn a right triangle ABC , right angled at B, the ratio of AB→AC is 1:√2 . Find the values of 2tanA1+tan2A and (ii) 2tanA1−tan2A
View Solution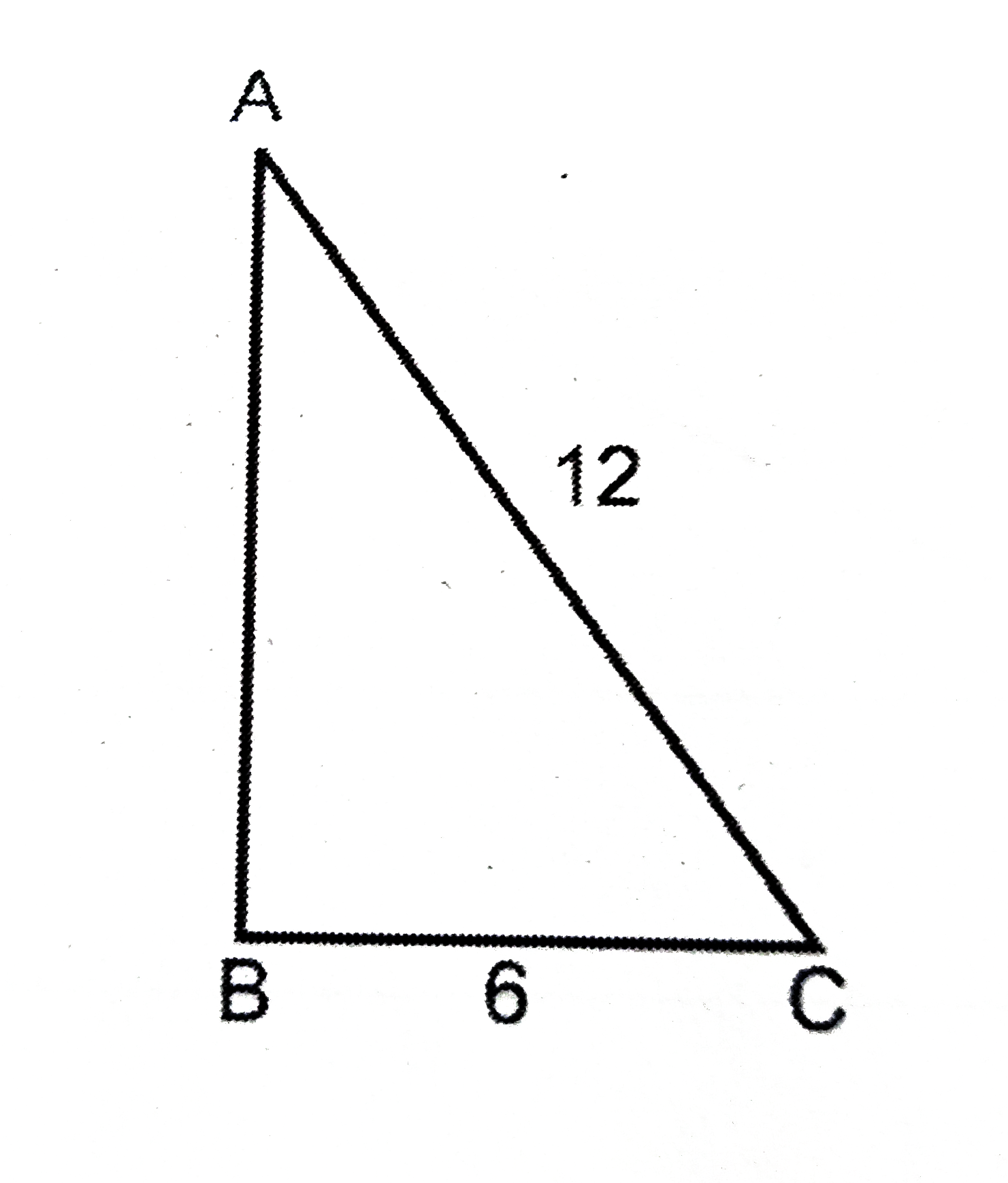
In the figure shown above, ABC is a triangle right angled at B. What is the value of angle A, in degrees?
View SolutionThe perimeter of a triangle ABC right angled at C is 70 and the inradius is 6, then |a−b|=
View Solution

