(i) What characteristic property of nuclear force explains the constancy of binding energy per nucleon (BE/A) in the range of mass number 'A' lying 30<A<170 ?
(ii) Show that the density of nucleus over a wide range of nuclei is constant-independent of mass number A.
To solve the given question, we will break it down into two parts as specified.
Part (i): Characteristic Property of Nuclear Force
1. Understanding Nuclear Force: The nuclear force is a strong interaction that holds protons and neutrons (nucleons) together in the nucleus. It is characterized by its short-range nature.
2. Short-Range Nature: The nuclear force acts effectively only at distances on the order of 1 femtometer (10^-15 meters). Beyond this range, the force diminishes rapidly and becomes negligible.
3. Independence from Charge: Unlike electromagnetic forces, the nuclear force does not depend on the charge of the nucleons. It is attractive and acts equally between protons and neutrons.
4. Binding Energy per Nucleon: The binding energy per nucleon (BE/A) remains approximately constant for mass numbers in the range of 30 < A < 170. This is due to the saturation property of the nuclear force, meaning that each nucleon interacts with a fixed number of neighboring nucleons, leading to a relatively uniform binding energy.
5. Conclusion: The characteristic property of the nuclear force that explains the constancy of binding energy per nucleon in this mass range is its short-range nature and saturation effect.
Part (ii): Density of Nucleus
1. Density Definition: The density (ρ) of a nucleus is defined as its mass (M) divided by its volume (V). Mathematically, this can be expressed as:
ρ=MV
2. Volume of the Nucleus: The volume of a spherical nucleus can be calculated using the formula for the volume of a sphere:
V=43πR3
where R is the radius of the nucleus.
3. Radius of the Nucleus: The radius of a nucleus can be approximated using the formula:
R=R0A1/3
where R0 is a constant (approximately 1.1 femtometers).
4. Substituting Radius into Volume: Substituting the expression for R into the volume formula gives:
V=43π(R0A1/3)3=43πR30A
5. Mass of the Nucleus: The mass of the nucleus can be approximated as:
M=A×mn
where mn is the mass of a nucleon (approximately 1 amu or 1.67×10−27 kg).
6. Density Calculation: Now substituting the expressions for mass and volume into the density formula:
ρ=MV=A×mn43πR30A
Simplifying this gives:
ρ=3mn4πR30
7. Conclusion: The density of the nucleus is independent of the mass number A, as it cancels out in the equation. The density remains approximately constant across a wide range of nuclei.
Final Result for Density
Calculating the numerical value, we find:
ρ≈3×1017 kg/m3
This value is consistent for various nuclei, confirming that nuclear density is approximately constant regardless of the mass number A.
ρ=MV
V=43πR3
where R is the radius of the nucleus.
R=R0A1/3
where R0 is a constant (approximately 1.1 femtometers).
V=43π(R0A1/3)3=43πR30A
M=A×mn
where mn is the mass of a nucleon (approximately 1 amu or 1.67×10−27 kg).
ρ=MV=A×mn43πR30A
Simplifying this gives:
ρ=3mn4πR30
Calculating the numerical value, we find:
ρ≈3×1017 kg/m3
This value is consistent for various nuclei, confirming that nuclear density is approximately constant regardless of the mass number A.
Similar Questions
Draw the graph showing thervariation of binding energy per nucleon with mass number. Give therason for the decrease of binding energy per nucleon for nuclei with high mass numbers.

The binding energy per nucleon for nuclei with high mass number is low due to the large coulomb repulsion between the protons inside these nuclei.
View SolutionAs the mass number A increases, the binding energy per nucleon in a nucleus.
View SolutionAssertion The binding energy per nucleon, for nuclei with atomic mass number A>100, decreases with A.
Reason The nuclear forces are weak for heavier nuclei.
View SolutionAssume that the nuclear binding energy per nucleon (B/A) versus mass number (A) is as shown in the figure. Use
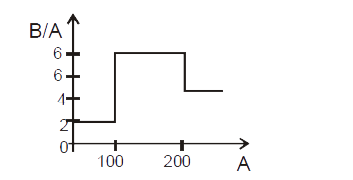
this plot to choose the correct choice(s) given below. Figure
View SolutionUsing the curve for the binding energy per nucleon as a function of mass number A, state clearly how the release in energy in the processes of nuclear fission and nuclear fusion can be explained.
View SolutionAssume that the nuclear binding energy per nucleus(B/A) versus mass number (A) is as shown in the figure Use this plot to choose the correct (s) choice given below

View SolutionDraw a plot of the binding energy per nucleon as a function of mass number for a large number of nuclei , 2≤A≤240 . How do you explain the constancy of binding energy per nucleon in the range 30<A<170 using the property that nuclear force is short-ranged ?
View Solution(a) Explain the processes of nuclear fission and nuclear fusion by using the plot of binding energy per nucleon (BE/A) versus the mass number A.
(b) A radioactive isotope has a hald -life of 10 years. How long will it take for the activity to reduce to 3.125%.
View SolutionAssertion : Binding energy per unit nucleon increase in atomic mass number .
Reason : Density of nucleus increases with increase in mass number.
View SolutionAssume that the nuclear binding energy per nucleon (B/A) versus mass number (A) is as shown in figure. Use this plot to choose the correct choice(s) given below.
(a) Fusion of two nuclei with mass numbers, lying in the range of 1<A<50 will release energy.
Fusion of two nuclei with mass numbers lying in the range of 51<A<100 will release energy.
(c) Fission of a nucleus lying in the mass range of 100<A<200 will release energy when broken into two equal fragements.
(d) Fission of a nucleus lying in the mass range of 200<A<260 will release energy when broken into two equal fragments.
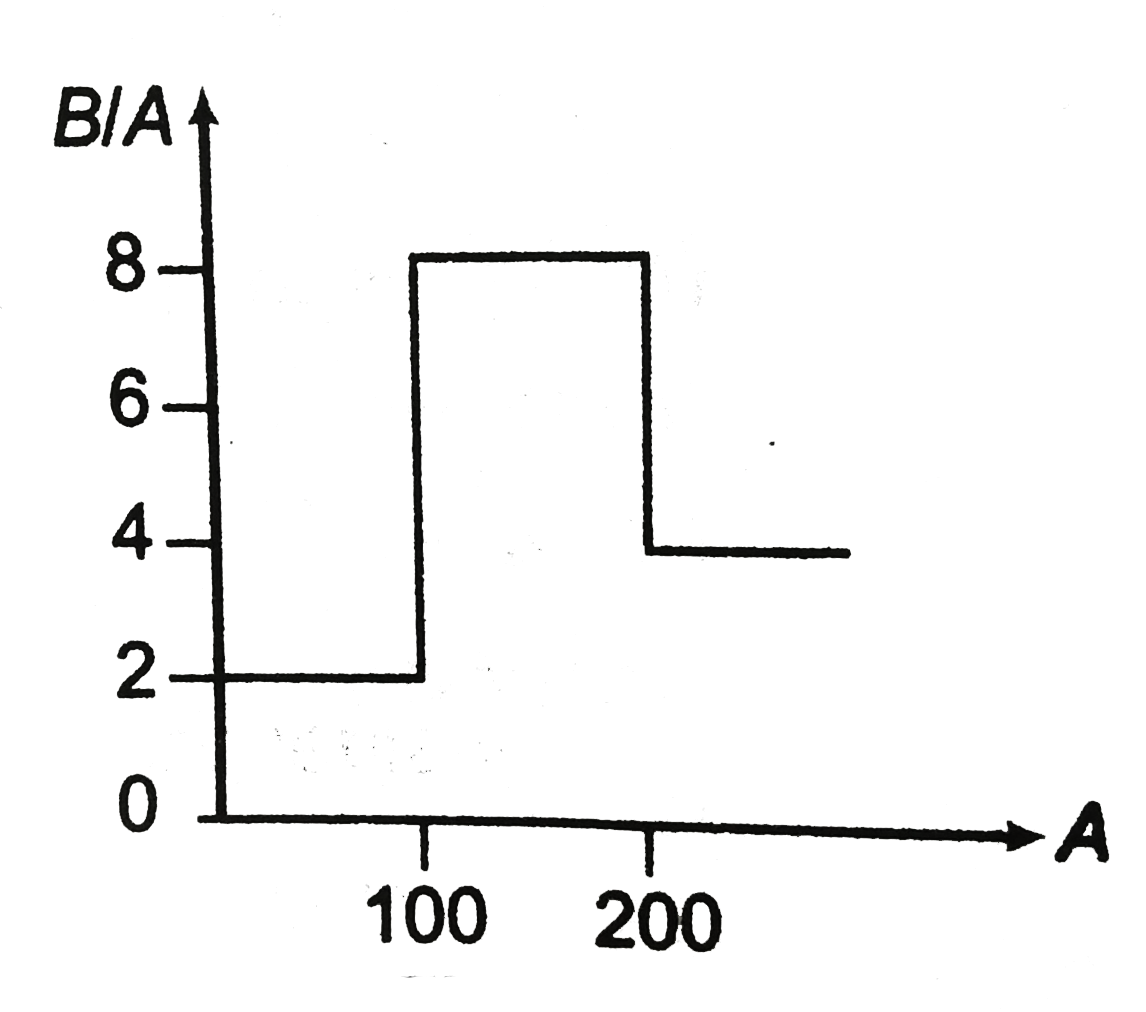
View Solution

