Calculate the time required to deposit 1.27 g of copper at cathode when a current of 2A was passed through the solution of CuSO4.
(Molar mass of Cu=63.5gmol−1,1F=96500Cmol−1).
To calculate the time required to deposit 1.27 g of copper at the cathode when a current of 2 A is passed through a solution of CuSO₄, we can use Faraday's first law of electrolysis. Here’s a step-by-step solution:
Step 1: Determine the Equivalent Weight of Copper
The equivalent weight (E) can be calculated using the formula:
E=Molar massn
where:
- Molar mass of Cu = 63.5 g/mol
- n (number of electrons transferred) for the reduction of Cu²⁺ to Cu = 2
So,
E=63.5g/mol2=31.75g/equiv
Step 2: Calculate the Electrochemical Equivalent (Z)
Using Faraday's law, the electrochemical equivalent (Z) is given by:
Z=EF
where:
- F (Faraday's constant) = 96500 C/mol
Thus,
Z=31.75g/equiv96500C/mol≈3.29×10−4g/C
Step 3: Use Faraday’s First Law to Find Time (t)
According to Faraday's first law:
Weight deposited=Z⋅I⋅t
Rearranging for time (t):
t=Weight depositedZ⋅I
Substituting the values:
- Weight deposited = 1.27 g
- I = 2 A
So,
t=1.27g(3.29×10−4g/C)⋅(2A)
Step 4: Calculate the Time
Calculating the denominator:
Z⋅I=3.29×10−4g/C⋅2A=6.58×10−4g/s
Now substituting back into the equation for time:
t=1.27g6.58×10−4g/s≈1930s
Final Answer
The time required to deposit 1.27 g of copper at the cathode is approximately 1930 seconds.
---
The equivalent weight (E) can be calculated using the formula:
E=Molar massn
where:
- Molar mass of Cu = 63.5 g/mol
- n (number of electrons transferred) for the reduction of Cu²⁺ to Cu = 2
E=63.5g/mol2=31.75g/equiv
Using Faraday's law, the electrochemical equivalent (Z) is given by:
Z=EF
where:
- F (Faraday's constant) = 96500 C/mol
Z=31.75g/equiv96500C/mol≈3.29×10−4g/C
According to Faraday's first law:
Weight deposited=Z⋅I⋅t
Rearranging for time (t):
t=Weight depositedZ⋅I
Substituting the values:
- Weight deposited = 1.27 g
- I = 2 A
t=1.27g(3.29×10−4g/C)⋅(2A)
Calculating the denominator:
Z⋅I=3.29×10−4g/C⋅2A=6.58×10−4g/s
t=1.27g6.58×10−4g/s≈1930s
The time required to deposit 1.27 g of copper at the cathode is approximately 1930 seconds.
Similar Questions
(a) Calculate the mass of Ag deposited at cathode when a current of 2 amperes was passed through a solution of AgNO3 for 15 minutes
(Given : Molar mass of Ag=108gmol−11F=96500Cmol−1)
(b) Define fuel cell
View SolutionHow much copper is deposited on the cathode if a current of 3A is passed through aqueous CuSO4 solution for 15 minutes?
View SolutionThe strength of 11.2 volume solution of H2O2 is:
[Given that molar mass of H = 1 g mol−1andO=16gmol−1]
View Solution(a) A steady current of 2 amperes was passed through two electrolytic cells X and Y connected in series containing electrolytes FeSO4 and ZnSO4 until 2.8 g of Fe deposited at the cathode of cell X. How long did the current flow ? Calculate the mass of Zn deposited at the cathode of cell Y
(Molar mass : Fe= 56 g mol−1 Zn-65.3g mol−1, 1F -96500 C mol−1)
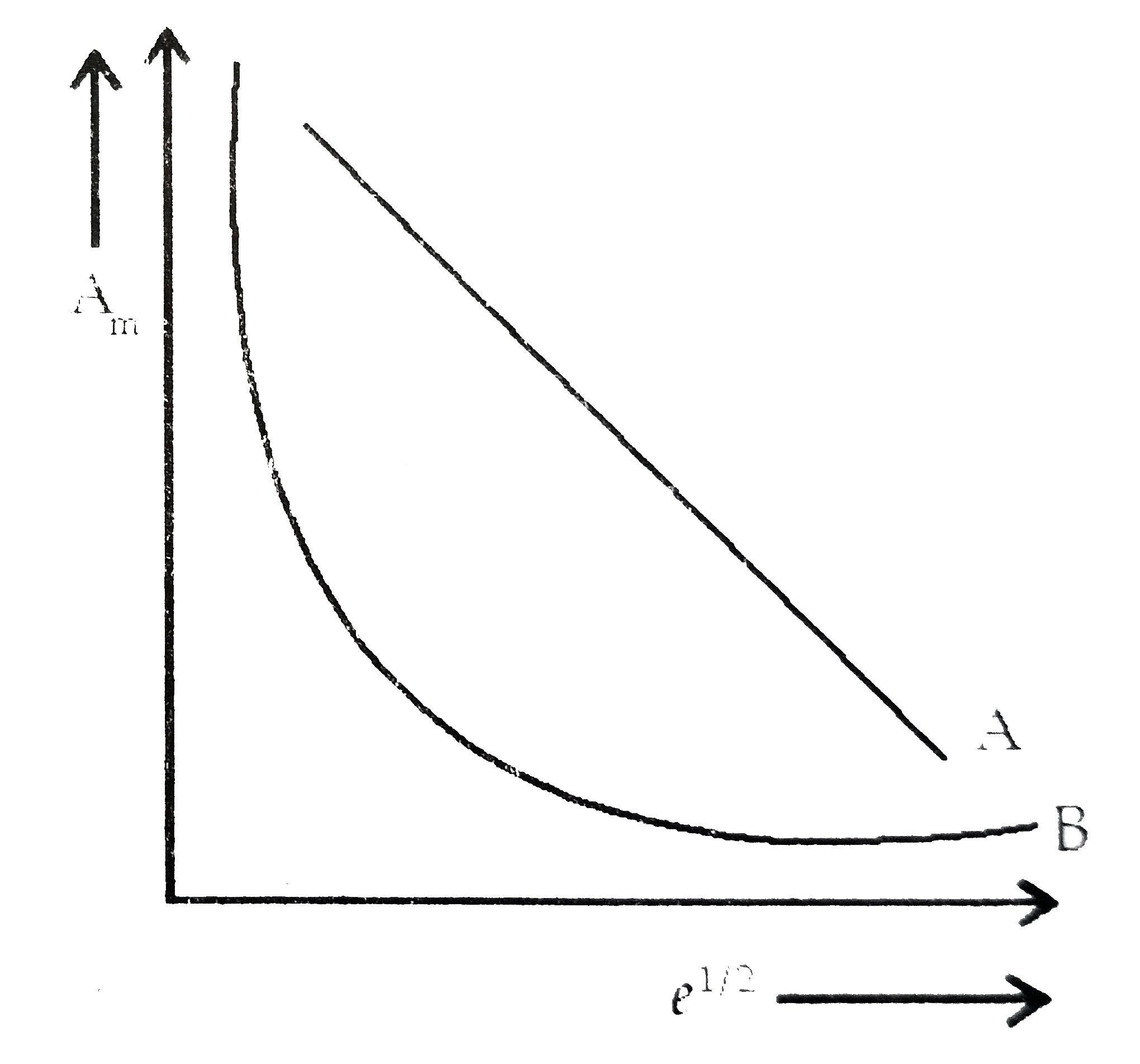
(b) In the plot of molar conductivity (∧m) vs Square root of concentration (c1/2), following curves are obtained for two electrolytes.
A and B:
Answer the following : (i) Predict the nature of electrolytes A and B. (ii) What happens on extrapolation of ∧m to concentration approaching zero for electrolytes A and B ?
View SolutionA current of 2A was passed for 1.5 hours through a solution of CuSO4 when 1.6g of copper was deposited. Calculate percentage current efficiency.
View SolutionA current of 1.50 A was passed through an electrolytic cell containing AgNO3 solution with inert electrodes. The weight of silver deposited was 1.50g. How long did the current flow ? (Molar mass of Ag=108g mol −1,1F=96500C mol−1).
View SolutionTwo faraday of electricity is passed through a solution of CuSO4. The mass of copper deposited at the cathode is: (at mass of Cu = 63.5 amu)
View SolutionCalculate the moles of methanol in 5 litres of its 2m solution, if the density of the solution is 0.981 kg L−1. (Molar mass = 32.0 g mol−1).
View SolutionCalculate the number of coulombs required to deposit 5.4g of Al when the electrode reaction is :
Al3++3e−→Al [Atomic weight of Al = 27 g/mol]
View SolutionIf 965 coulombs of electricity is passed through a metal cup dipped in silver(l) salt solution, in order to plate it with silver. Then the amount of silver deposited on its surface is (Given : the molar mass of Ag=108gmol−1,1F=96500 coulombs)
View Solution
