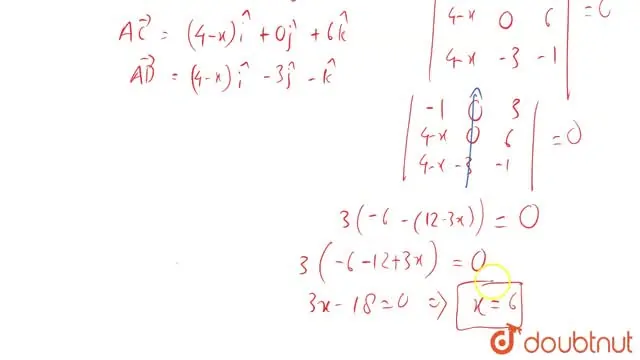Using vectors, find the value of x such that the four points A(x,5,-1), B(3,2,1), C(4,5,5) and D(4,2,-2) are coplanar.
Step by step video & image solution for Using vectors, find the value of x such that the four points A(x,5,-1), B(3,2,1), C(4,5,5) and D(4,2,-2) are coplanar. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Find x such that the four points A (3, 2, 1), B(4,x, 5), C (4, 2, 2)and D (6, 5, 1)are coplanar
View SolutionShow that the points A(−1, 4, −3), B(3, 2, −5), C(−3, 8, −5)and D(−3, 2, 1) are coplanar.
View SolutionPlot the points A(4,2),B(−5,3),C(−4,−5)andD(5,−2).
View SolutionUsing vectors, find the area of the triangle with vertices A(1,1,2), B(2,3,5)and C(1,5,5)
View SolutionUsing vectors, find the area of the triangle with vertices A(1,1,2), B(2,3,5)and C(1,5,5)
View SolutionUsing vectors, find the area of the triangle with vertices A(1,1,2), B(2,3,5)and C(1,5,5)
View SolutionFind the value of λ. If the points A(−1,3,2),B(−4,2,−2) and C(5,λ,10) are collinear.
View SolutionFind the value of x for which the points (x−1), (2,1)and (4,5) are collinear.
View SolutionUsing vectors, find the area of the ΔABC with vertices A(1, 2, 3), B(2, -1, 4) and C(4, 5, -1)
View SolutionUsing vectors, find the area of the triangle with vertices A (1, 1, 2), B (2, 3, 5) and C (1, 5, 5).
View Solution