Find the eqution of the curve passing through the point (1,1), if the tangent drawn at any point P(x,y) on the curve meets the coordinate axes at A and B such that P is the mid point of AB.
The below figure obtained by the given information
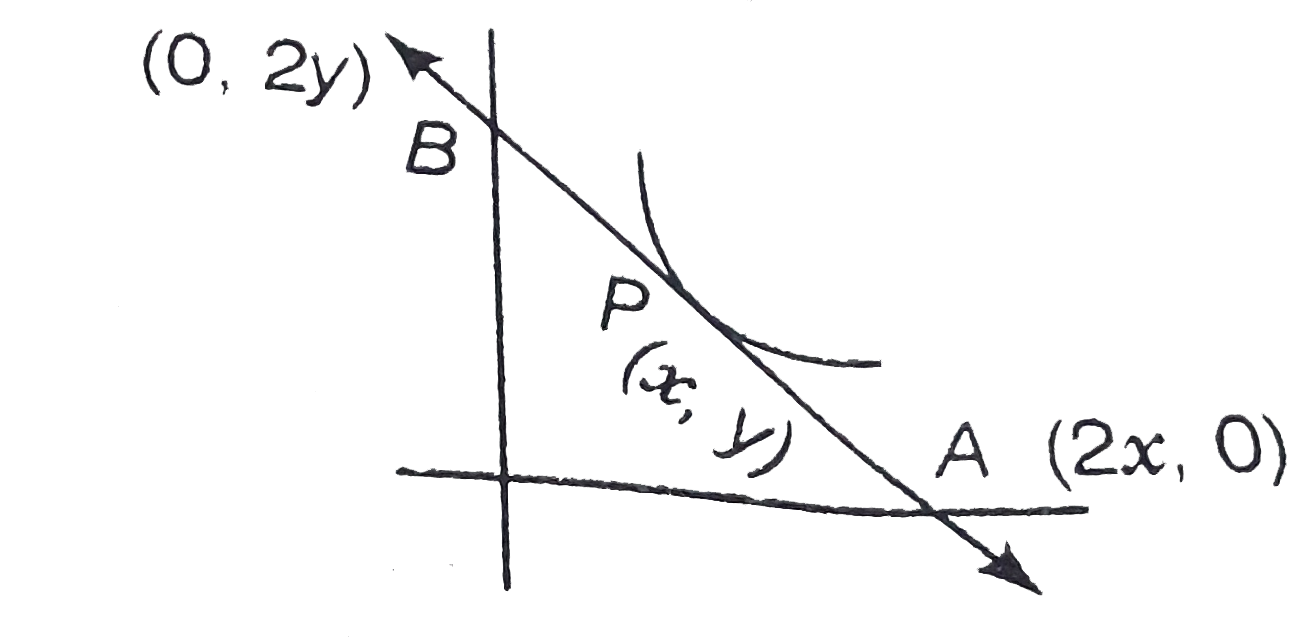
Let the coordinate of the point P is (x, y). It is given that, P is mid-point of AB.
So, the coordinates of points A and B are (2x, 0) and (0, 2y), respectively.
∴ Slope of AB=0−2y2x−0=−yx
Since, the segment AB is a tangent to the curve at P.
∴ dydx=−yx
⇒ dyy=−dxx
On integrating both sides, we get
logy=−logx+logC
logy=logCx ...(i)
Since, the given curve passes through (1, 1).
∴ log1=logC1
⇒ 0=logC
⇒ c=1
∴ logy=log1x
⇒ y=1x
⇒ xy=1
Similar Questions
The tangent at any point P on the circle x2+y2=4 meets the coordinate axes at AandB . Then find the locus of the midpoint of AB.
View SolutionFind the equation of the curve passing through the point (0, -2) given that at any point (x,y) on the curve the product of the slope of its tangent and y coordinate of the point is equal to the x-coordinate of the point.
View SolutionFind the equation of a curve passing through (1,1) and whose slope of tangent at a point (x, y) is −xy.
View SolutionFind the equation of a curve passing through the point (0,1) if the slope of the tangent to the curve at any point (x,y) is equal to the sum of the x coordinate (abscissa) and the product of the x coordinate and y coordinate (ordinate) of that point.
View SolutionFind the equation of the curve passing through the point (1,0) if the slope of the tangent to the curve at any point (x,y)isy−1x2+x.
View SolutionFind the equation of a curve passing through the point (0, 1). If the slope of the tangent to the curve at any point (x, y) is equal to the sum of the x coordinate (abscissa) and the product of the x coordinate and y coordinate (ordinate) of that point.
View SolutionFind the equation of a curve passing through the point (0, 1). If the slope of the tangent to the curve at any point (x, y) is equal to the sum of the x coordinate (abscissa) and the product of the x coordinate and y coordinate (ordinate) of that point.
View SolutionFind the equation of a curve passing through the point (0, 1). If the slope of the tangent to the curve at any point (x, y) is equal to the sum of the x coordinate (abscissa) and the product of the x coordinate and y coordinate (ordinate) of that point.
View SolutionFind the equation of the curve through the point (1,0), if the slope of the tangent to the curve at any point (x,y) is y−1x2+x
View SolutionFind the equation of the curve passing through the point, (5,4) if the sum of reciprocal of the intercepts of the normal drawn at any point P(x,y) on it is 1.
View Solution


