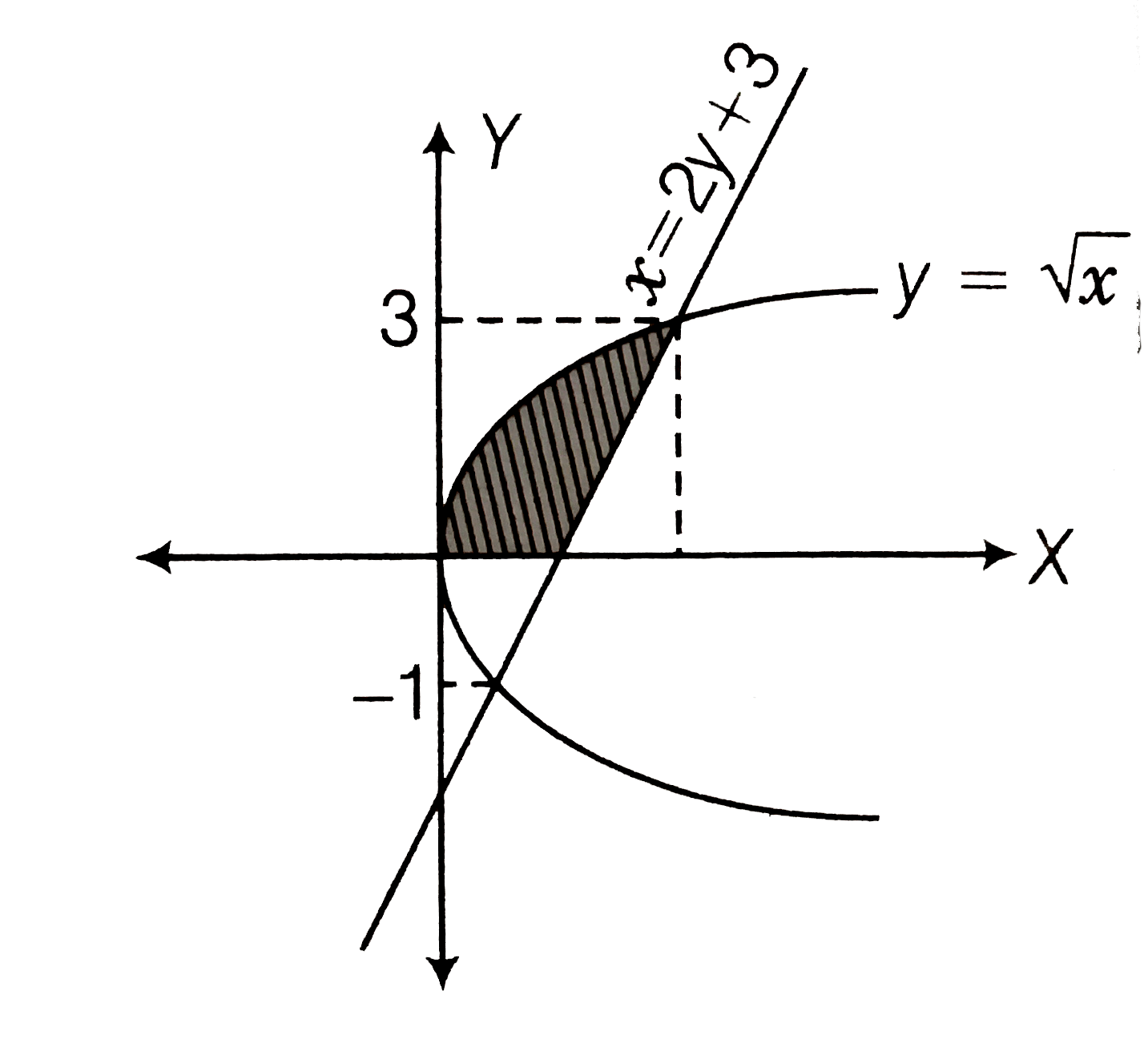
Find the area bounded by the curve $y = \sqrt{x}, x = 2 y + 3$ in the first quadrant and X-axis.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:N/a

Given equation of the curves are $y = \sqrt{x} and x = 2 y + 3$ in the first quadrat.
On solving both the equations for y, we get
$y = \sqrt{2 y + 3}$
$\Rightarrow y^{2} = 2 y + 3$
$\Rightarrow y^{2} - 2 y - - 3 = 0$
$\Rightarrow y^{2} - 3 y + y - 3 = 0$
$\Rightarrow y (y - 3) + 1 (y - 3) = 0$
$\Rightarrow (y - 1) (y - 3) = 0$
$\Rightarrow y = - 1, 3$
$∴ Required area of shaded region,$
$A = \int_{0}^{3} (2 y + 3 - y^{2}) d y = {[\frac{2 y^{2}}{2} + 3 y - \frac{y^{3}}{3}]}_{0}^{3}$
$= [\frac{18}{2} + 9 - 9 - 0] = 9 sq units$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-APPLICATION OF INTEGRALS-Objective Type Questions

Home
Ask Doubt
Profile