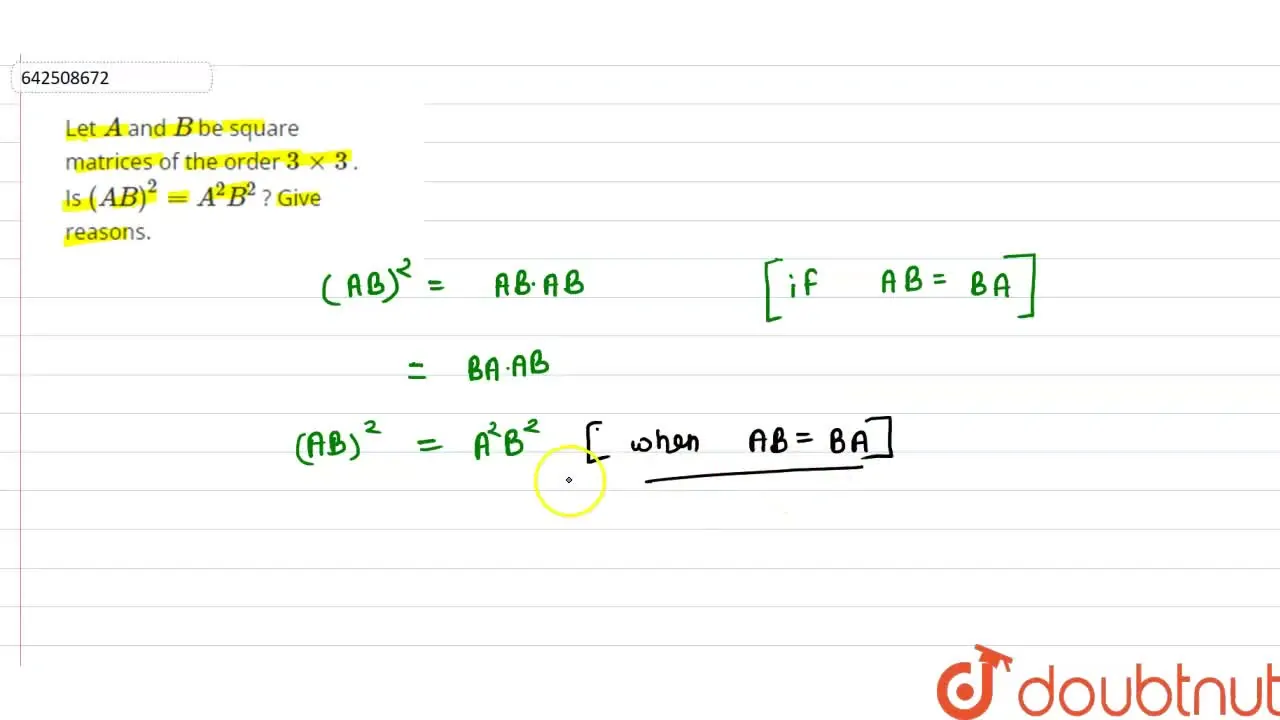
Let A and B be square matrices of the order 3×3 . Is (AB)2=A2B2 ? Give reasons.
Since A and B are square matrices of order 3×3
AB2=ABAB
=AB AB
=A A B B [∵AB=BA]
=A2B2
So, AB2=A2B2 is true when AB=BA.
Related Playlists
Similar Questions
If A and B are square matrices of order 3, then
View SolutionIf A and B are square matrices of the same order then (A+B)2=A2+2AB+B2 implies
View SolutionLet A and B be square matrices of the same order. Does (A+B)2=A2+2AB+B2 hold? If not, why?
View SolutionIf A and B are two square matrices of the same order, then A+B=B+A.
View SolutionLet A,B and C be square matrices of order 3×3 with real elements. If A is invertible and (A−B)C=BA−1, then
View SolutionLet A and B be square matrices of the same order such that A2=I and B2=I, then which of the following is CORRECT ?
View SolutionIf A and B are square matrices of same order, then (A+B) (A-B) is equal to
View Solutionif A and B are two matrices of order 3×3so that AB=A and BA=B then (A+B)7=
View SolutionIf A and B are square matrices of the same order, explain, why in general (A+B)2≠A2+2AB+B2 (ii) (A−B)2≠A2−2AB+B2 (iii) (A+B)(A−B)≠A2−B2 .
View SolutionState with reason, whether the following are true of false. A, B and C are matrices of order 2×2.
(A−B)2=A2−2A.B+B2.View Solution