Suppose that 6% of the people with blood group O are left handed and 10% of those with other blood groups are left handed, 30 % of the people have blood groups O. If a left handed person os selected at random, what is the probability that he/she will have blood group O?
To solve the problem, we need to find the probability that a randomly selected left-handed person has blood group O. We will use Bayes' theorem for this calculation.
1. Define Events:
- Let E1 be the event that the selected person has blood group O.
- Let E2 be the event that the selected person has a blood group other than O.
- Let E be the event that the selected person is left-handed.
2. Given Information:
- Probability of blood group O, P(E1)=0.30
- Probability of other blood groups, P(E2)=1−P(E1)=1−0.30=0.70
- Probability of being left-handed given blood group O, P(E|E1)=0.06
- Probability of being left-handed given other blood groups, P(E|E2)=0.10
3. Apply Bayes' Theorem:
We want to find P(E1|E), the probability that a left-handed person has blood group O. According to Bayes' theorem:
P(E1|E)=P(E|E1)⋅P(E1)P(E|E1)⋅P(E1)+P(E|E2)⋅P(E2)
4. Calculate the Numerator:
P(E|E1)⋅P(E1)=0.06⋅0.30=0.018
5. Calculate the Denominator:
- First calculate P(E|E2)⋅P(E2):
P(E|E2)⋅P(E2)=0.10⋅0.70=0.070
- Now, add both parts for the denominator:
P(E|E1)⋅P(E1)+P(E|E2)⋅P(E2)=0.018+0.070=0.088
6. Final Calculation:
P(E1|E)=0.0180.088=1888=944
Conclusion:
The probability that a randomly selected left-handed person has blood group O is 944.
- Let E1 be the event that the selected person has blood group O.
- Let E2 be the event that the selected person has a blood group other than O.
- Let E be the event that the selected person is left-handed.
- Probability of blood group O, P(E1)=0.30
- Probability of other blood groups, P(E2)=1−P(E1)=1−0.30=0.70
- Probability of being left-handed given blood group O, P(E|E1)=0.06
- Probability of being left-handed given other blood groups, P(E|E2)=0.10
We want to find P(E1|E), the probability that a left-handed person has blood group O. According to Bayes' theorem:
P(E1|E)=P(E|E1)⋅P(E1)P(E|E1)⋅P(E1)+P(E|E2)⋅P(E2)
P(E|E1)⋅P(E1)=0.06⋅0.30=0.018
- First calculate P(E|E2)⋅P(E2):
P(E|E2)⋅P(E2)=0.10⋅0.70=0.070
- Now, add both parts for the denominator:
P(E|E1)⋅P(E1)+P(E|E2)⋅P(E2)=0.018+0.070=0.088
P(E1|E)=0.0180.088=1888=944
The probability that a randomly selected left-handed person has blood group O is 944.
Topper's Solved these Questions
- PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:PROBABILITYExercise:Long Answer Type Questions
Explore 15 Videos
- PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:PROBABILITYExercise:Objective Type Questions
Explore 38 Videos
- MATRICESBook:NCERT EXEMPLAR ENGLISHChapter:MATRICESExercise:Solved example
Explore 101 Videos
- RELATIONS AND FUNCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Fillers
Explore 15 Videos
Similar Questions
Knowledge Check
What can be the blood group of offspring when both parents have AB blood group?
AA and B onlyBAB onlyCA, B, AB, and ODA, B, and ABWhat can be the blood group of offspring when both parents have AB blood group ?
AAB onlyBA,B and ABCA,B,AB and ODA and B only
What is correct for blood groups O?
View SolutionIn a medical examination of students of a class, the following blood groups are recorded.
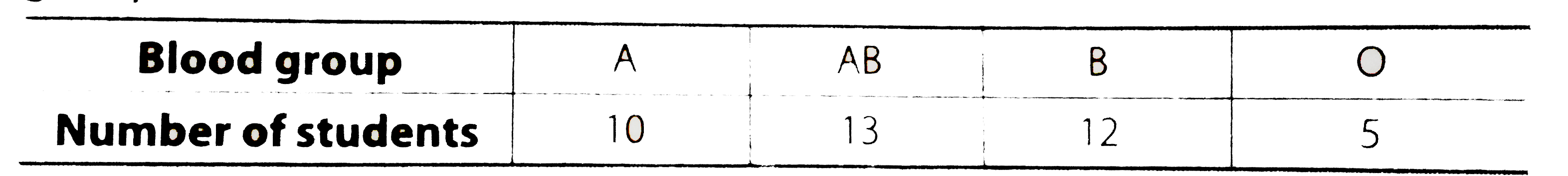
A student is selected at random from the class. The probability that he/she has blood group B, is
View SolutionProgeny with blood group 'O' can be obtained cross
View SolutionBlood group of a couple are AB and O. The possible blood group of children would be
View SolutionA person having blood group 'O' can receive blood of :
View SolutionChildren of a father with 'O' blood group and mother with 'AB' blood group would be
View Solution

