If x is the number of tails in three tosses of a coin, then determine the standard deviation of X.
Given that, random variable X is the number of tails in three toses of the coin.
So, X=0,1,2,3.
⇒P(X=x)=nCx(p)xqn−x
Where n=3,p=1/2 andx=0,1,2,3
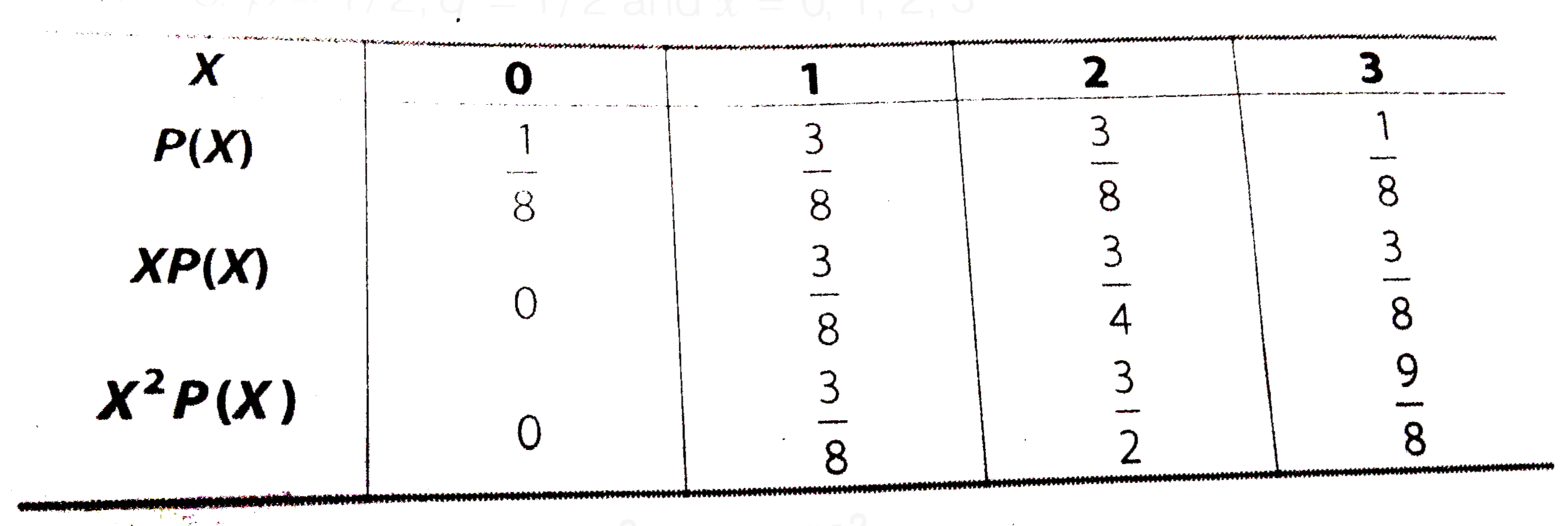
We know that, Var(X)=E(X2)−[E(X)]2
where, E(X2)=n∑i=1x2iP(xi)andE(X)=n∑i=1xiP(xi)
∴E(X2)=n∑i=1x2iP(Xi)=0+38+32+98=248=3
and [E(X)]2=[n∑i=0x2iP(xi)]2=[0+38+34+38]2=[128]2=94
∴Var(X)=3−94=34
and standard deviation of X=√Var(X)=√34=√32
Topper's Solved these Questions
- PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:PROBABILITYExercise:Long Answer Type Questions
Explore 15 Videos
- PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:PROBABILITYExercise:Objective Type Questions
Explore 38 Videos
- MATRICESBook:NCERT EXEMPLAR ENGLISHChapter:MATRICESExercise:Solved example
Explore 101 Videos
- RELATIONS AND FUNCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Fillers
Explore 15 Videos
Similar Questions
Find the mean number of heads in three tosses of a fair coin.
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionThe mean of getting tail two tosses of a coin is:
View SolutionFind the probability distribution of X; the number of heads in two tosses of a coin ( or a simultaneous toss of two coins).
View SolutionFind the probability distribution of (i) number of heads in two tosses of a coin. (ii) number of tails in the simultaneous tosses of three coins. (iii) number of heads in four tosses of a coin.
View SolutionFind the probability of getting tail each time in three tosses of a coin.
View SolutionLet X represent the difference between the number of heads and the number of tails obtained when a coin is tossed 6 times. What are possible values of X?
View SolutionLet x represent the difference between the number of heads and the numbers of tails obtained when a coin is tossed 4 times. Then possible values of X is
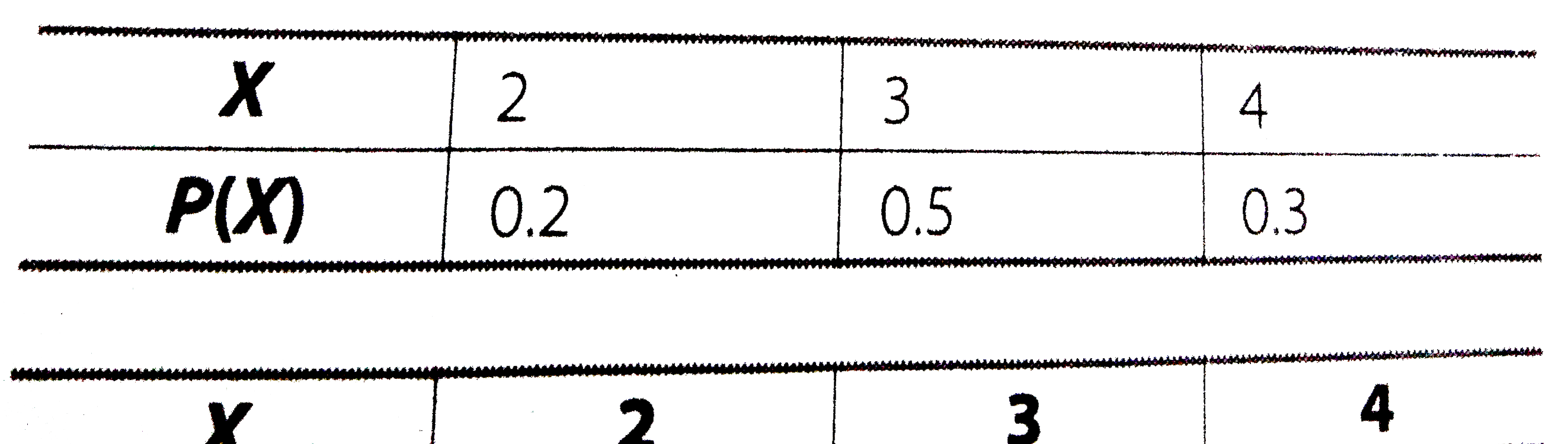
View SolutionFor the following probability distribution determine standard deviation of the random variable X.
View SolutionSuppose a girl throws a die. If she gets an even number, she tosses a coin three times and notes the number of 'tails'. If she gets an odd number, she tosses a coin once and notes whether a 'head' or 'tail' is obtained. If she obtained exactly one 'tail', what is the probability that she threw odd numbers with the die ?
View Solution

