A die has its six faces marked 0,1,1,1,6,6. Two such dice are thrown together and the total is recorded.
(i) How many different scores are possible
(ii) What is the probability of getting a total of 7 ?
Given, a die has its six faces marked {0,1,1,1,6,6}
∴ Total sample space, n(S)=(6)2=36
(i) The different score which are possible are 6 scores i.e. 0,1,2,6,7 and 12.
(ii) Let E=Event of getting a sum 7
={(1,6),(1,6),(1,6),(1,6),(1,6),(1,6),(6,1),(6,1),(6,1),(6,1),(6,1),(6,1)}
∴n(E)=12
∴P(E)=n(E)n(S)=1236=13
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ASWERS QUESTIONS14videos
STATISTICS AND PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - VERY SHORT ANSWERS QUESTIONS14videos
STATISTICS AND PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - REAL NUMBERSEXERCISE - LONG ANSWER TYPE QUESTIONS5videos
REAL NUMBERS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS20videos
SURFACE AREAS AND VOLUMES
Similar Questions
A die is thrown. Find the probability of getting: a number greater than 6 is 1.
View SolutionTwo dice are thrown together. Find the probability that the product the number on the top of the dice is
(i) 6 (ii) 12 (iii) 7View SolutionA pair of dice is thrown 6 times. If getting a total of 7 is considered a success, what is the probability of at least 5 successes .
View SolutionA pair of dice is thrown 7 times. If getting a total of 7 is considered a success, what is the probability of atmost 6 success?
View SolutionA child has die whose six faces show the letters as given below:
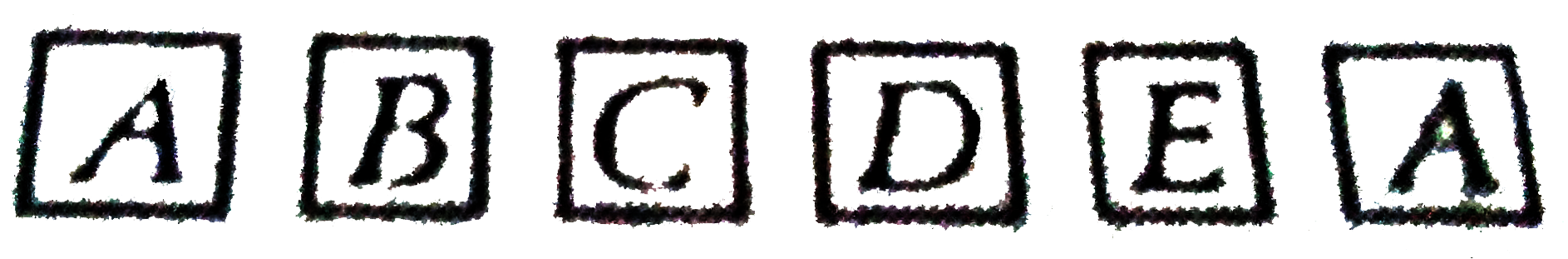
The die is thrown once. What is the probability of getting (i) A, (ii) D?View SolutionA die has 6 faces marked by the given numbers as shown below :

The die is thrown once. What is the probability of getting
(i) a positive integer.View SolutionA dice has 6 faces marked by the given below :
1, 2, 3, -1, -2, -3
The dice is thrown once. What is the probability of getting an integer greater than −3?View SolutionA dice has 6 faces marked by the given below :
1, 2, 3, -1, -2, -3
The dice is thrown once. What is the probability of getting a positive integer?View SolutionA die has 6 faces marked by the given numbers as shown below :

The die is thrown once. What is the probability of getting
(iii) the smallest integer.View SolutionA child has a die whose 6 faces show the letter as given below: A,B,C,A,A,B. The die is thrown once. What is the probability of getting (i) A (ii) B
View Solution


