Determine the maximum value of Z=11x+7y subject to the constraints 2x+y≤6,x≤2,x≥0,y≥0
Video Solution
Text Solution
The correct Answer is:N/a
We have maximise Z=11x+7y …(i)
Subject to the constraints
2x+y≤6….(ii)
x≤2….(iii)
x≥0,y≤0….(iv)
We see that, the feasible region as shaded determined by the system of constraints (ii) to (iv) is OABC and is bounded. So, now we shall corner point method to determine the maximum value of Z.
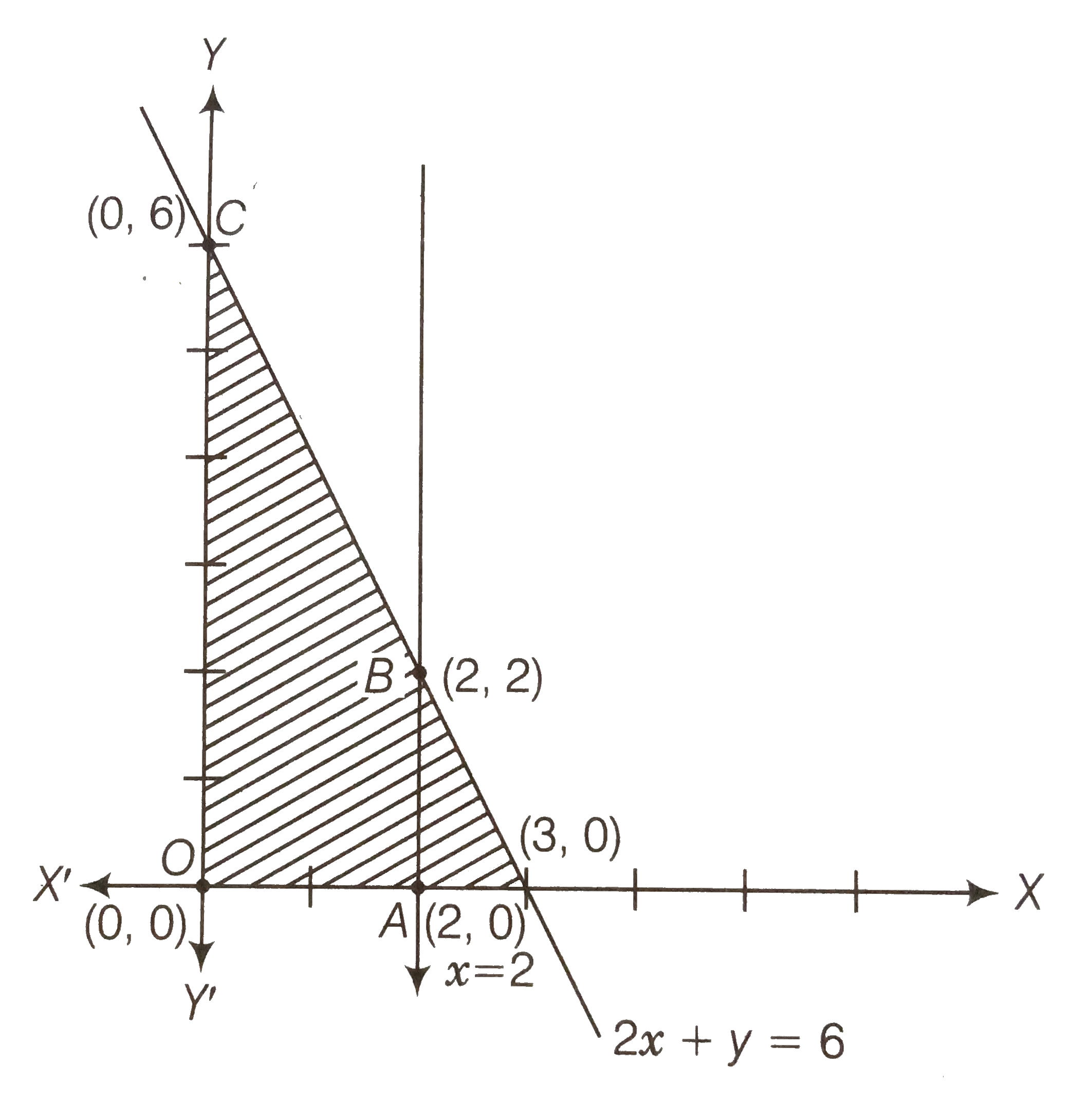

|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - OBJECTIVE8videos
LINEAR PROGRAMMING
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - FILLERS7videos
LINEAR PROGRAMMING
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Fillers18videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example101videos
MATRICES
Similar Questions
Maximise the function Z=11x+7y, subject to the constraints x≤3,y≤2,x≥0,y≥0
View Solution2x+y≤6,x+2y≤8,x≥0,y≥0
View Solutiony−2x≤1,x+y≤2,x≥0,y≥0
View Solutionx−y≤2,x+y≤4,x≥0,y≥0
View Solution2x+y≥6,x+2y≥8,x≥0,y≥0
View SolutionMinimise Z=13x-15y subject to the constraints x+y≤7,2x−3y+6≥0,x≥0,x≥0,andy≥0
View SolutionFind graphically the minimum value of Z = 100x + 50y, subject to the constraints x+y≤300,3x+y≤600,y≤x+200,x≥0,y≥0.
View SolutionMaximise Z=3x+4y, Subjected to the constraints x+y≤1,x≥0,y≥0
View Solutionx+y≤10,4x+3y≤24,x≥0,y≥0
View Solution2x+y≥0
View Solution
