(Cosine Formulae) if a,b,c are the lengths of the sides opposite respectively to the angles A,B,C of a triangle ABC, show that (I) cosA=b2+c2−a22bc (ii) cosB=c2+a2−b22ac (iii) (i) cosC=a2+b2−c22ab
Here, components of C are c cos A and c sin A is drawn.
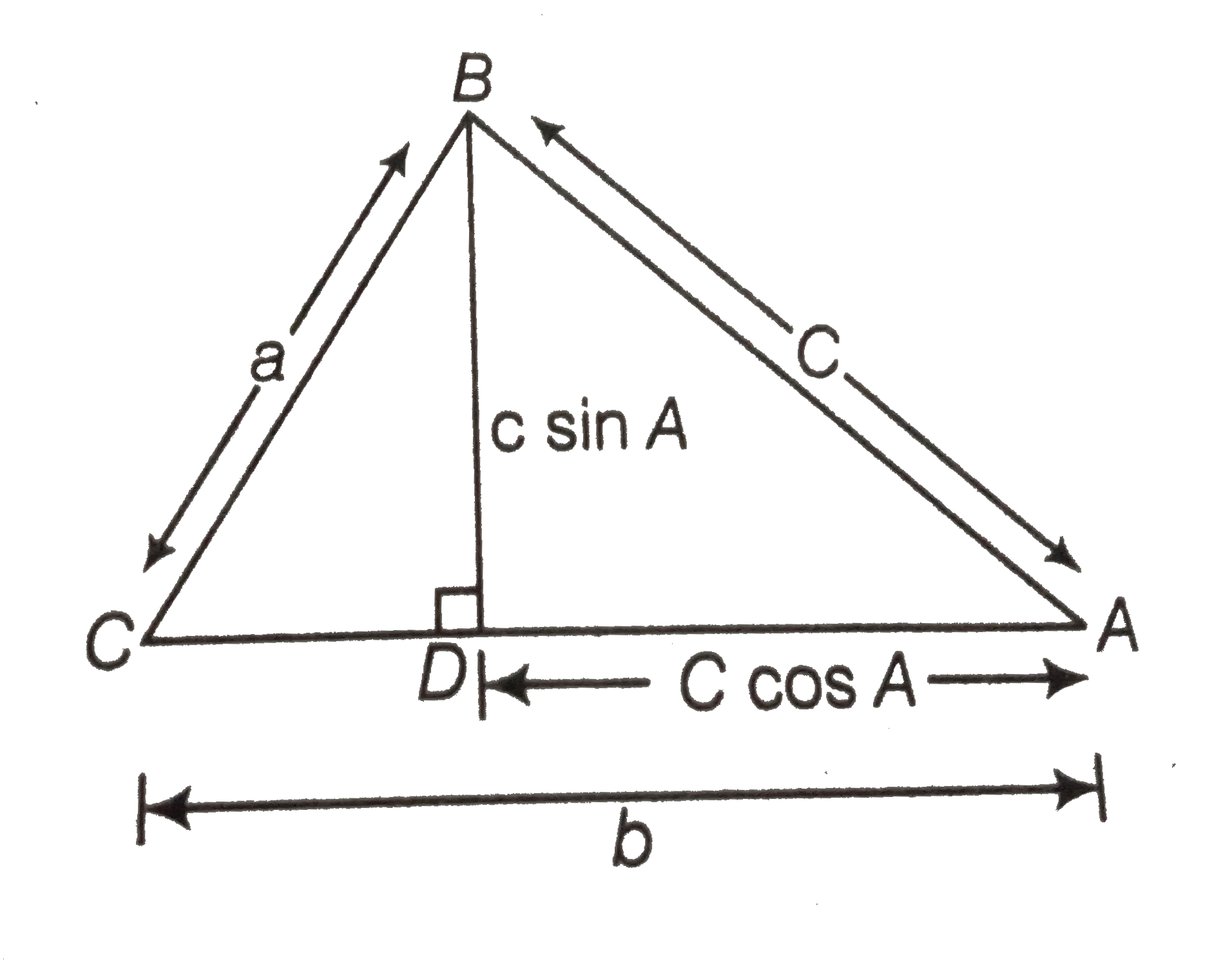
Since, −−→CD=b−ccosA
In ΔBDS a2=(b−cosA)2+(csinA)2
⇒a2=b2+c2cos2A−2bccosA+c2sin2A
⇒2bccosA=b2−a2+c2(cos2Asin2A)
∴cosA=b2+c2−a22ab
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - OBJECTIVE TPYE QUESTIONS
27 Videos
- VECTOR ALGEBRABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - OBJECTIVE TPYE QUESTIONS
27 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - LONG ANSWER TYPE QUESTIONS
16 Videos
Similar Questions
(Cosine Formulae) if a,b,c are the lengths of the sides opposite respectively to the angles A,B,C of a triangle ABC, show that cosAb2+c2−a22bc (ii) cosBc2+a2−b22ac (iii) (i) cosCa2+b2−c22ab
View SolutionIf any triangle ABC , that: b2−c2cosB+cosC+c2−a2cosC+cosA+a2−b2cosA+cosB=0
View SolutionIn any triangle ABC prove that: sin(B−C2)=(b−ca)cosA2
View SolutionFor any triangle ABC, prove thatcosAa+cosBb+cosCc=a2+b2+c22abc
View SolutionIn any triangle ABC, prove that: sin(B−C)sin(B+C)=b2−c2a2
View SolutionIn a △ABC, acosB + b cosC + c cosA =a+b+c2 then
View SolutionIn any ΔABC, prove that: a(b cosC−ccosB)=b2−c2
View SolutionIf A, B and C are interior angles of a triangle ABC, then show that sin(B+C2)=cosA2 .
View SolutionIn any ΔABC, prove that: cosAa+cosBb+cosCc=a2+b2+c22abc
View SolutionIf A, B, C are the interior angles of a triangle ABC , prove that tan(C+A2)=cotB2 (ii) sin(B+C2)=cosA2
View Solution
