Simplify each of the following: ${cos}^{- 1} (\frac{3}{5} cos x + \frac{4}{5} sin x)$ , where $- \frac{3 π}{4} \leq x \leq \frac{π}{4}$ ${sin}^{- 1} (\frac{5}{13} cos x + \frac{12}{13} sin x)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:N/a

We have, ${cos}^{- 1} [\frac{3}{5} cos x + \frac{4}{5} sin x], x \in [\frac{- 3 π}{4}, \frac{π}{4}]$
Let $cos y = \frac{3}{5}$
$\Rightarrow sin y = \frac{4}{5}$
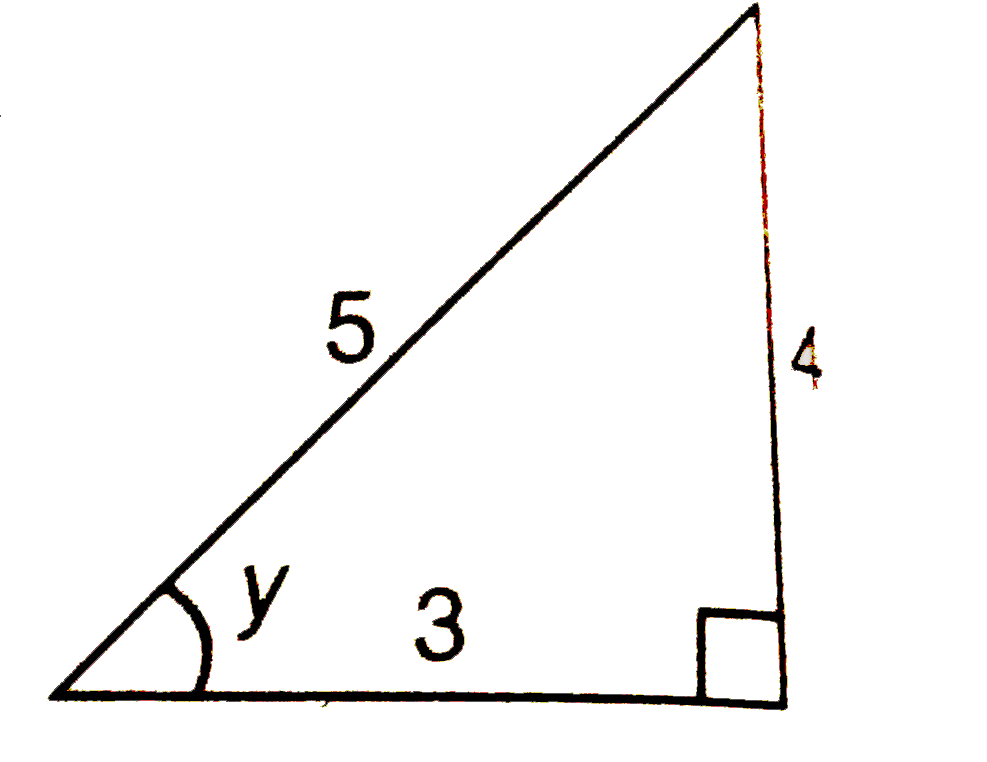
$\Rightarrow y = {cos}^{- 1}' \frac{3}{5} = {sin}^{- 1}' \frac{4}{5} = {tan}^{- 1}' (\frac{4}{3})$
${cos}^{- 1} [cos y . cos x + sin y . sin x]$
$= {cos}^{- 1} [cos (y - x)], [∵ cos (A - B) = cos A . cos B + sin A . sin B]$
$= y - x = {tan}^{- 1}' \frac{4}{3} - x$ , $[∵ y = {tan}^{- 1}' \frac{4}{3}]$

Updated on:21/07/2023

|

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-INVERSE TRIGONOMETRIC FUNCTIONS-Fillers

Home
Ask Doubt
Profile