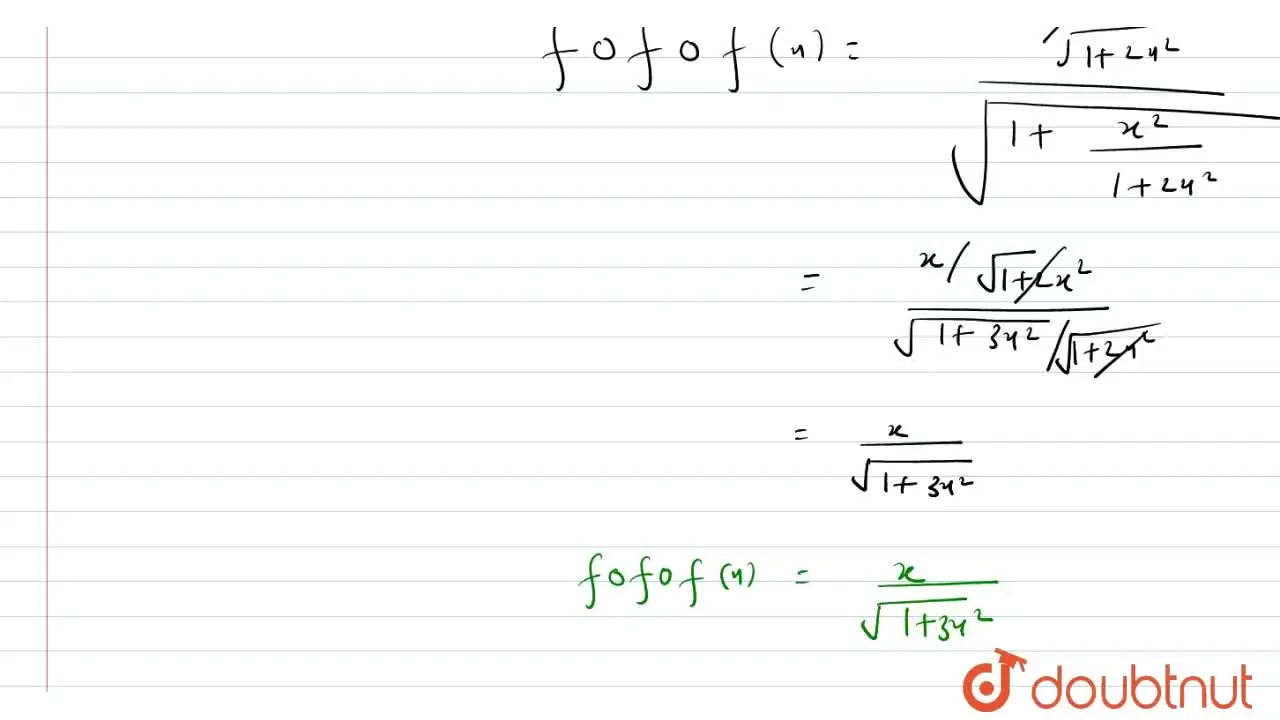If f:R→R be defined by f(x)=x√1+x2, then (fofof)(x)=…………..
Video Solution
Text Solution
The correct Answer is:N/a
Given that, f(x)=x√1+x2
(fofof)(x)=f[f{f(x)}]
=f[f(x√1+x2)]=f⎛⎜
⎜
⎜
⎜⎝x√1+x2√1+x21+x2⎞⎟
⎟
⎟
⎟⎠
=f⎡⎢
⎢
⎢
⎢⎣x√1+x2√1+x2(√2x2+1)⎤⎥
⎥
⎥
⎥⎦=f(x√1+2x2)
=x√1+2x2√1+x21+2x2=x√1+2x2√1+2x2√1+3x2
=x√1+3x2=x√3x2+1
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Objective Type Questions20videos
RELATIONS AND FUNCTIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - True/False9videos
PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - LONG ANSWER TYPE QUESTIONS16videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
If f(x)=x√1+x2 then fofof(x)
View SolutionIf f(x)=x√1+x2 then fofof(x)
View Solutionf:R→R defined by f(x)=x2+5
View SolutionIf f:R→R be defined by f(x)=1x,∀x∈R. Then , f is
View SolutionIf f:R→R is defined by f(x)=x2−3x+2, write f{f(x)}.
View SolutionIf f:R→R defined by f(x)=x2+1 , then find f−1(−3)
View SolutionLet f:R→R be a function defined by f(x)=x2−8x2+2. Then f is
View SolutionLet f:R→R be a function defined by f(x)=x2−x21+x2. Then:
View SolutionIf f:R→R be a function defined as f(x)=x2−8x2+2, then f is
View SolutionIf f:R→R defined as f(x)=3x+7, then find f−1(−2)
View Solution