Question

If the line $lx+my-1=0$
touches the circle $x^2+y^2=a^2$
, then prove that $(l,m)$
lies on a circle.

Explanation

True
Given circle is `x^(2)+y^(2)=a^(2)`
`therefore` Radius of circle=a and centre =(0,0)

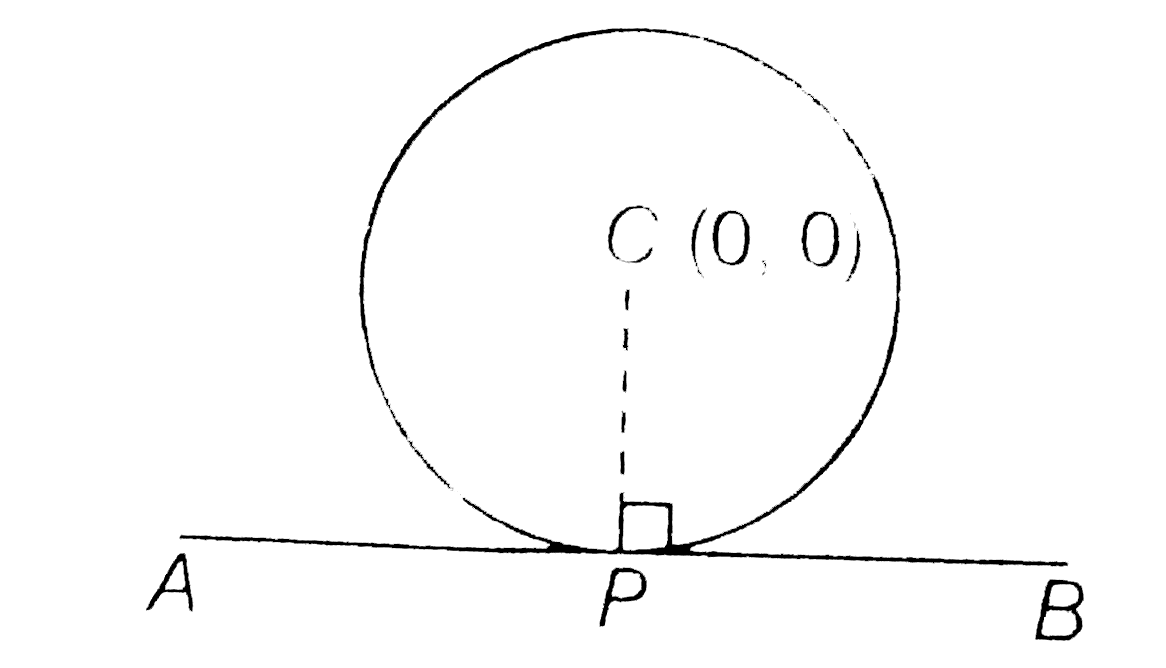
`therefore` Distance from point (l,m) and centre is `sqrt((0-e)^(2)+(0-m)^(2))`=a
`rArr l^(2)+m^(2)=a^(2)`
So, l,m lie on the circle.