If o be the sum of odd terms and E that of even terms in the expansion of (x+a)n prove that: O2−E2=(x2−a2)n (ii) 4OE=(x+a)2n−(x−a)2n (iii) 2(O2+E2)=(x+a)2n+(x−a)2n
(i) Given expansin is (x+a)n
∴(x+a)n=.nC0xna0+.nC1xn−1a1+.nC2xn−2a2+.nC3xn−3a3+....+.nCnan
Now, sum of odd terms
i.e., O=.nC0xn+.nC2xn−2a2+....
i.e., E=.nC1xn−1a+.nC3xn−3a3+.....
∴(x+a)n=O+E....(i)
Similarly (x−a)n=O−E .....(ii)
.:(O+E)(O−E)=(x+a)n(x−a)n [on multiplying Eqs. (i) and (ii)]
⇒O2−E2=(x2−a2)n
(ii) 4OE=(O+E)2−(O−E)2=[(x+a)n]2−[(x−a)n]2 [from Eqs. (i) and (ii)]
=(x+a)2n−(x−a)2n
Topper's Solved these Questions
- BINOMIAL THEOREMBook:NCERT EXEMPLAR ENGLISHChapter:BINOMIAL THEOREMExercise:Objective type question
Explore 16 Videos
- BINOMIAL THEOREMBook:NCERT EXEMPLAR ENGLISHChapter:BINOMIAL THEOREMExercise:True/False
Explore 7 Videos
- BINOMIAL THEOREMBook:NCERT EXEMPLAR ENGLISHChapter:BINOMIAL THEOREMExercise:True/False
Explore 7 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:NCERT EXEMPLAR ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:OBJECTIVE TYPE QUESTIONS
Explore 16 Videos
Similar Questions
If o be the sum of odd terms and E that of even terms in the expansion of (x+a)n prove that: (i)O2−E2=(x2−a2)n (ii) 4OE=(x+a)2n−(x−a)2n (iii) 2(O2+E2)=(x+a)2n+(x−a)2n
View SolutionIf A be the sum of odd terms and B that of even terms in the expansion of (x+a)n prove that: A2−B2=(x2−a2)n
View SolutionIf P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, prove that
(i) p2−Q2=(x2−a2)n
View SolutionIf P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, prove that
(iii) 2(P2+Q2)=(x+a)2n+(x−a)2n.
View SolutionIf A be the sum of odd terms and B be the sum of even terms in the expansion of (x+a)n, prove that A2−B2=(x2−a2)n
View SolutionIf A be the sum of odd terms and B the sum of even terms in the expnsion of (x+a)n,show that 4AB= (x+a)2n−(x−a)2n
View SolutionIf the sum of odd terms and the sum of even terms in the expansion of (x+a)n are p and q respectively then p2+q2=
View SolutionIf P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, prove that
(ii) 4PQ=(x+a)2n−(x−a)2nand
View Solution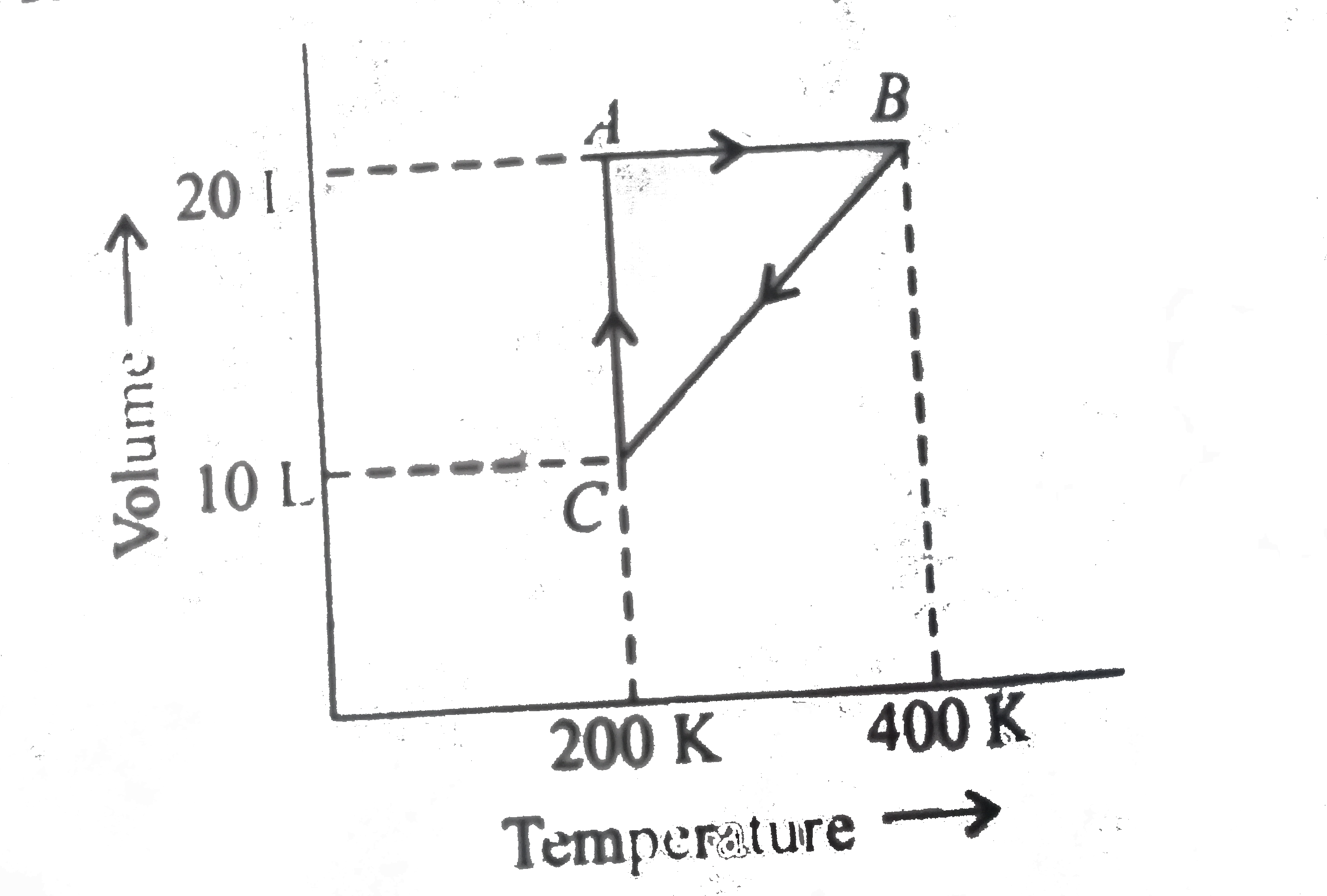
The pressures at A and B in the atmosphere are, respectively,
View SolutionIf the sum of odd terms and the sum of even terms in the expansion of (x+a)n are p and q respectively then p2−q2=
View Solution

