If n is an odd positive integer, show that (n2−1) is divisible by 8.
Video Solution
Text Solution
Let a=n2−1 …(i)
Given that, n is an odd integer n=1,3,5…
From Eq. (i), at n=1, a =(1)2−1=1−1−0,
Which is divisible by 8.
From Eq. (i), atn=3,a=(3)2−1=9−1=8
which is divisibly by 8.
From Eq. (i), at n=5, a=(5)2−1=25−1=24=3×8
Which is divisible by 8
From Eq. (i), at n=7, a=(7)2−1=49−1=48=6×8
Which is divisible by 8.
Hence, (n2−1) is divisibly by 8m where n is an odd integer.
Alternate Method
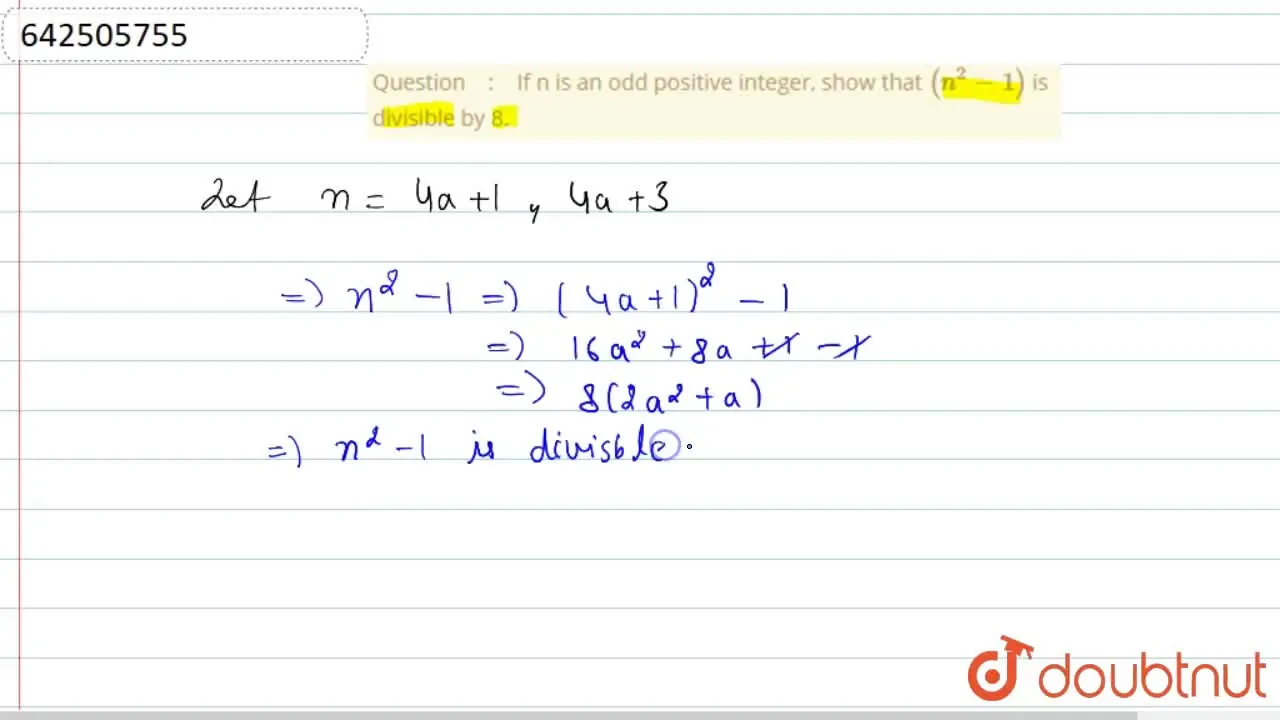
We know that that an odd integer n is of the from (4q+1)or(4q+3) for some integer q.
CASE I When m=4q+1
In this case, we have (n2−1)=(4q+1)2−1
=16q2+1+8q−1 [∴(a+b)2=a2+2ab+b2]
=16q2+8q=8q(2q+1)
=16(q2+8q=8q(2q+1)
Which is clearly, divisibly by 8.
CASE II When n=4p+3
In this case, we have
(n2−1)=(4q+3)2−1
=16q2+9+24q−1 [∴(a+b)2=a2+2ab+b2]
=16q2+24q+8
=8(2q2+3q+1)
which is clearly divisibly by 8.
Hence, (n2−1) is divisibly by 8.
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - REAL NUMBERSEXERCISE - LONG ANSWER TYPE QUESTIONS5videos
REAL NUMBERS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - REAL NUMBERSEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS10videos
REAL NUMBERS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRIATIC EQUATIONSEXERCISE - LONG ANSWER TYPE12videos
QUADRIATIC EQUATIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ASWERS QUESTIONS14videos
STATISTICS AND PROBABILITY
Similar Questions
If n is a positive integer, show that 4n−3n−1 is divisible by 9
View SolutionIf n is a positive integer, show that: 4n−3n−1 is divisible by 9
View SolutionIf n is a positive integer, then show that 6n−5n−1 is divisible by 25
View SolutionIf n is an odd positive integer, then an+bn is divisible by
View SolutionIf n is a positive integer, prove that 33n−26n−1 is divisible by 676.
View SolutionIf n is a positive integer, show that: 32n−1+24n−32n2 is divisible by 512 if n>2
View Solutionn2−1 is divisible by 8, if n is
View SolutionIf n is positive integer show that 9n+7 is divisible 8
View SolutionIf n is any positive integer , show that
23n+3−7n−8 is divisible by 49 .View SolutionIf n is a positive integer, then show tha 32n+1+2n+2 is divisible by 7 .
View Solution