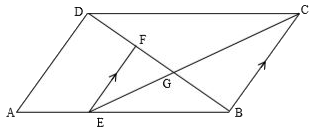
In the figure, it is given that BDEF and FDCE are parallelogram. Can you say that BD = CD ? Why or why not?
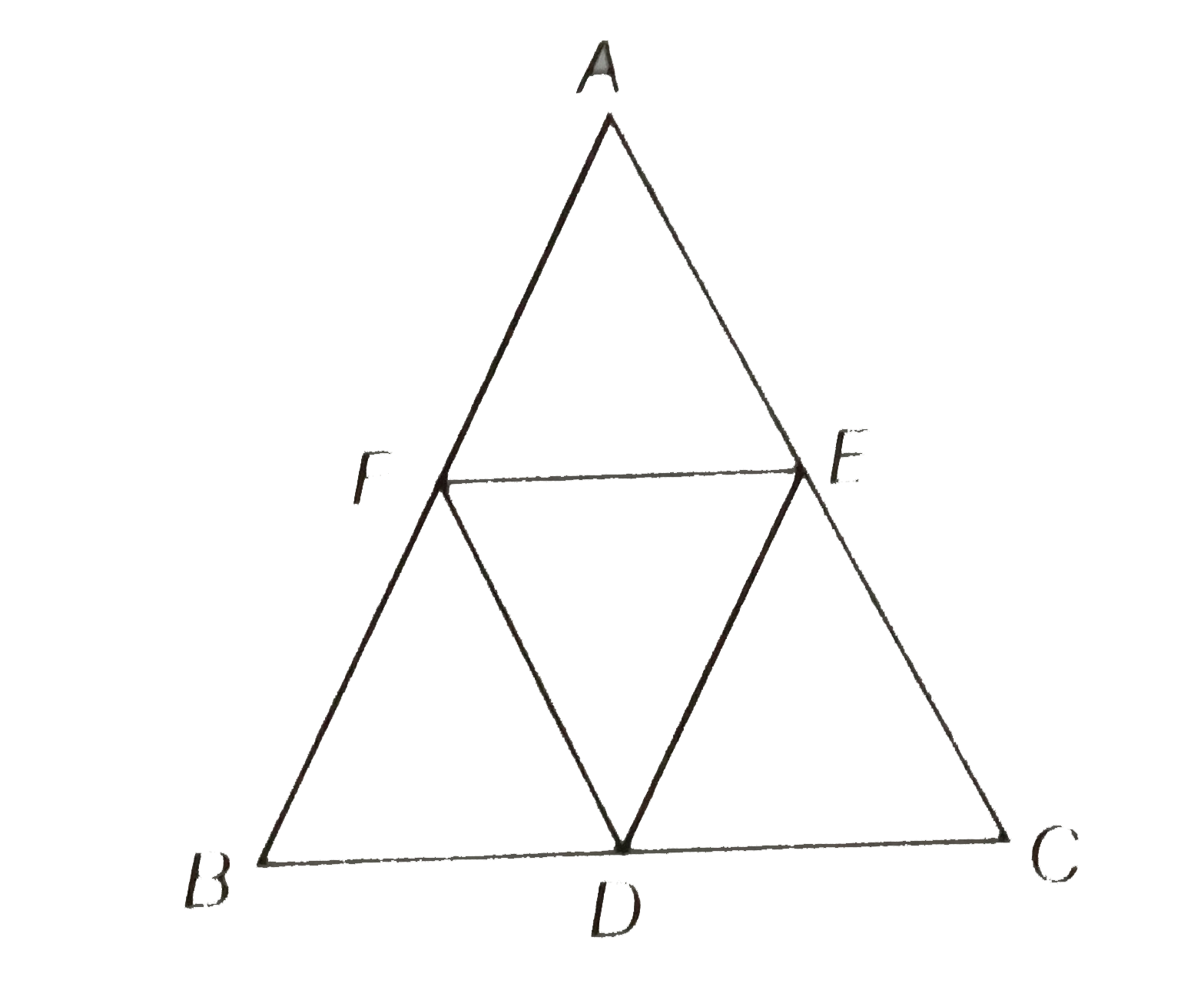
Yes, in the given figure, BDEF is a parallelogram.
Also, FDCE is a parallelogram.
and CD = EF …(ii)
From Eqs. (i) and (ii), BD = CD = EF
Topper's Solved these Questions
- QUADRILATERALS Book:NCERT EXEMPLAR ENGLISHChapter:QUADRILATERALS Exercise:SHORT ANSWER TYPE QUESTIONS
Explore 10 Videos
- QUADRILATERALS Book:NCERT EXEMPLAR ENGLISHChapter:QUADRILATERALS Exercise:LONG ANSWER TYPE QUESTIONS
Explore 18 Videos
- QUADRILATERALS Book:NCERT EXEMPLAR ENGLISHChapter:QUADRILATERALS Exercise:LONG ANSWER TYPE QUESTIONS
Explore 18 Videos
- POLYNOMIALSBook:NCERT EXEMPLAR ENGLISHChapter:POLYNOMIALSExercise:EXERCISE 2.4 Long Answer type Questions
Explore 9 Videos
- STATISTICS AND PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:STATISTICS AND PROBABILITYExercise:LONG ANSWER TYPE QUESTIONS
Explore 12 Videos
Similar Questions
In Figure, BDEF and DCEF are each a parallelogram. Is it true that BD=DC? Why or why not?
View SolutionIt is given that ΔABC≅ΔRPQ .Is it true to say that BC =QR ? Why ?
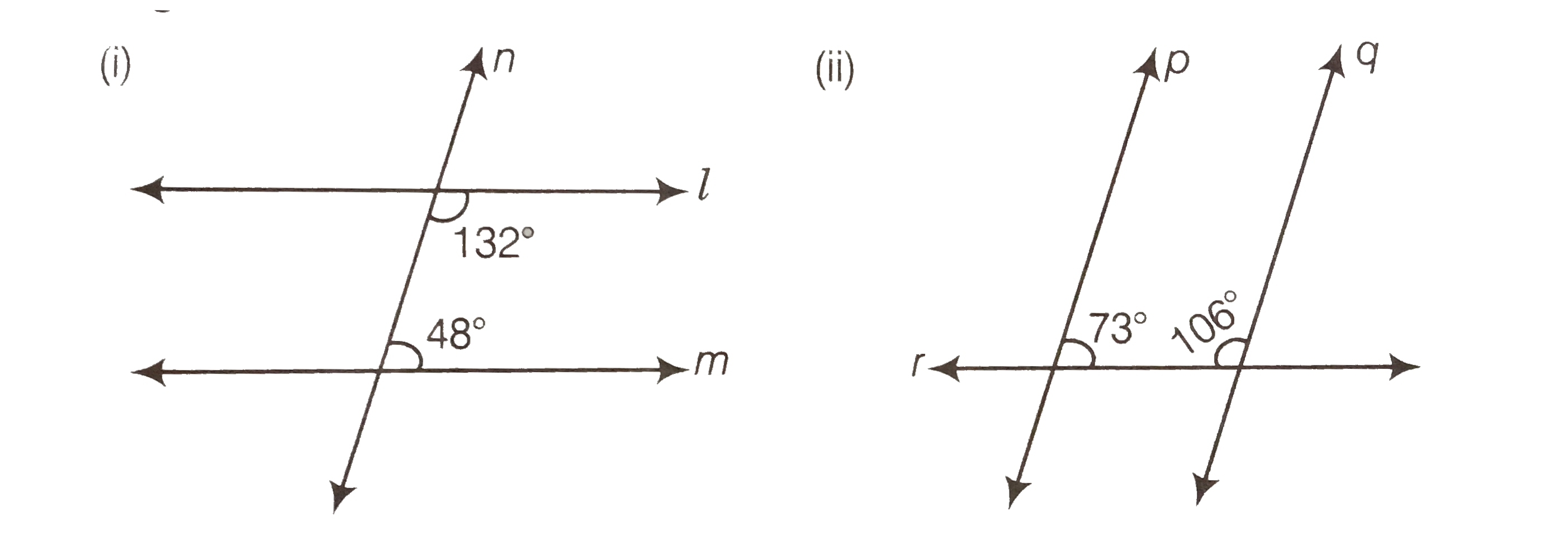
View SolutionIn the figure, which of the two lines are parallel and why ?
View SolutionIn the given figure AC = BD, prove that AB = CD.

View SolutionThe diagonals of a parallelogram are not perpendicular. Is it a rhombus? Why or why not?
View SolutionIn fig 7.13, AD=CDandAB=CB. (i) state the three pairs of equal in ΔABDandΔCBD. (iii) Is ΔABD[≡~?]ΔCBD ? Why or why not ? (iii) Does BD bisect ? ABC ? Given reasons
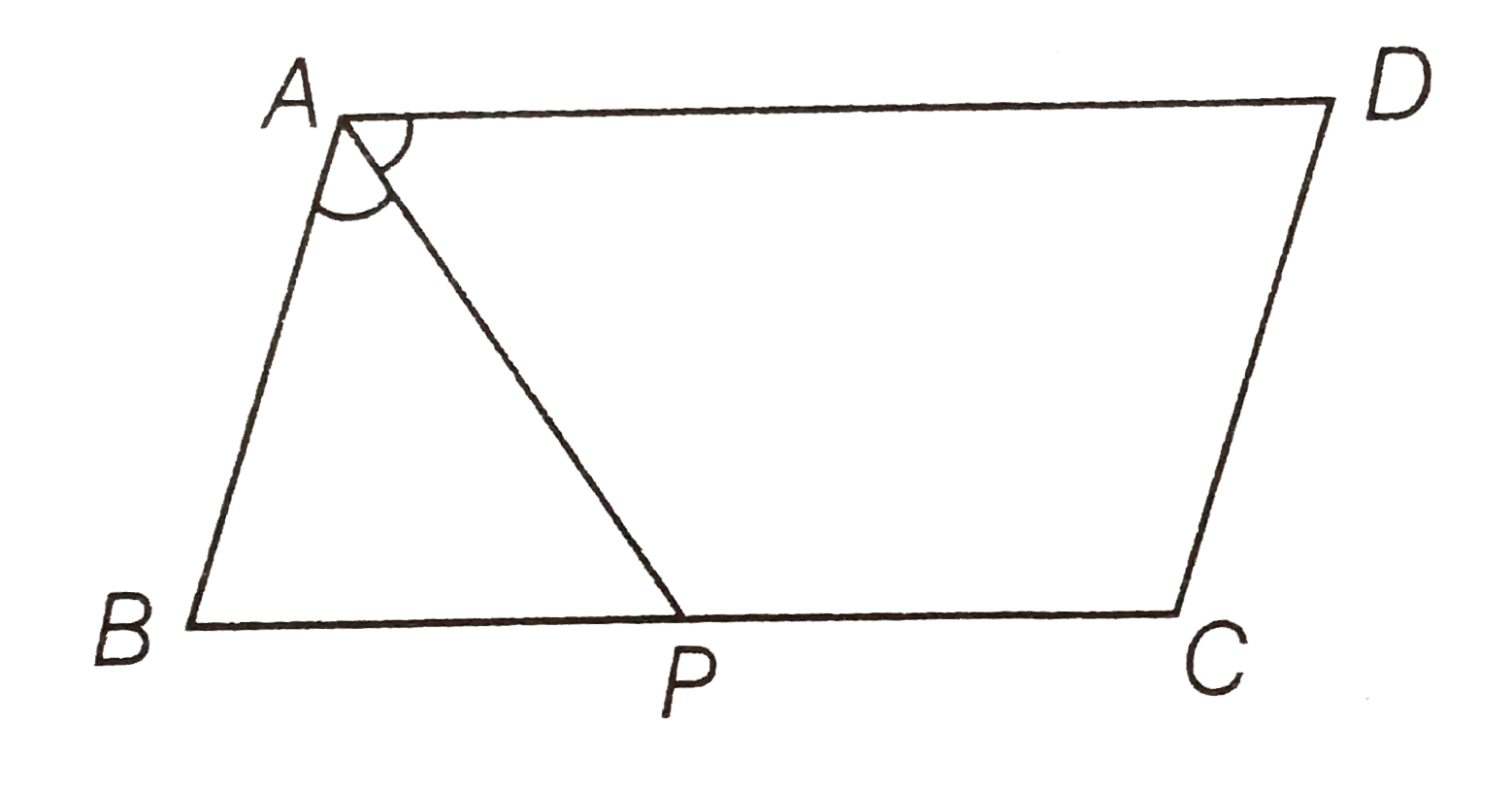
View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD.
View SolutionIn the given figure, ABCD is a parallelogram. Find the area of ΔAED

View SolutionIn the figure given below, ABCD is a parallelogram. E is a point on AB. CE intersects the diagonal BD at G and EF is parallel to BC.
If AE : EB = 1 : 2 find
EF : AD
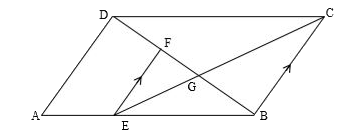
View SolutionIn the figure given below, ABCD is a parallelogram. E is a point on AB. CE intersects the diagonal BD at G and EF is parallel to BC.
If AE : EB = 1 : 2 find
area of triangle BEF : area of triangle ABD
View Solution

