Four candidates A, B, C, D have applied for the assignment ot coach a school cricket team. If A is twice as likely to be selected as B, and B and C are given about the same chance of being selected, while C is twice as likely to be selected as D, what are the probability that (i) C will be selected ? (ii) A will not be selected?
To solve the problem, we will define the probabilities of candidates A, B, C, and D based on the information given and then calculate the required probabilities.
1. Define Probabilities:
- Let the probability of candidate B be P(B)=k.
- Since A is twice as likely to be selected as B, we have:
P(A)=2k
- B and C are given about the same chance of being selected, so:
P(B)=P(C)=k
- C is twice as likely to be selected as D, thus:
P(C)=2P(D)⟹P(D)=k2
2. Sum of Probabilities:
- The sum of the probabilities of all candidates must equal 1:
P(A)+P(B)+P(C)+P(D)=1
- Substituting the expressions we have:
2k+k+k+k2=1
3. Combine Terms:
- Combine the terms on the left:
2k+k+k+k2=4k+k2=8k2+k2=9k2
- Therefore, we have:
9k2=1
4. Solve for k:
- Multiply both sides by 2:
9k=2⟹k=29
5. Calculate Individual Probabilities:
- Now we can find the probabilities for each candidate:
- P(A)=2k=2×29=49
- P(B)=k=29
- P(C)=k=29
- P(D)=k2=2/92=19
6. Answer the Questions:
- (i) The probability that C will be selected:
P(C)=29
- (ii) The probability that A will not be selected:
P(A′)=1−P(A)=1−49=59
Final Answers:
- (i) The probability that C will be selected is 29.
- (ii) The probability that A will not be selected is 59.
- Let the probability of candidate B be P(B)=k.
- Since A is twice as likely to be selected as B, we have:
P(A)=2k
- B and C are given about the same chance of being selected, so:
P(B)=P(C)=k
- C is twice as likely to be selected as D, thus:
P(C)=2P(D)⟹P(D)=k2
- The sum of the probabilities of all candidates must equal 1:
P(A)+P(B)+P(C)+P(D)=1
- Substituting the expressions we have:
2k+k+k+k2=1
- Combine the terms on the left:
2k+k+k+k2=4k+k2=8k2+k2=9k2
- Therefore, we have:
9k2=1
- Multiply both sides by 2:
9k=2⟹k=29
- Now we can find the probabilities for each candidate:
- P(A)=2k=2×29=49
- P(B)=k=29
- P(C)=k=29
- P(D)=k2=2/92=19
- (i) The probability that C will be selected:
P(C)=29
- (ii) The probability that A will not be selected:
P(A′)=1−P(A)=1−49=59
- (i) The probability that C will be selected is 29.
- (ii) The probability that A will not be selected is 59.
Topper's Solved these Questions
- PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Long Answer Type Questions
6 Videos
- PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Objective Type Questions
12 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTION EXERCISE - OBJECTIVE TYPE QUESTIONS
5 Videos
- RELATIONS AND FUNCTIONS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - True /False
5 Videos
Similar Questions
Three students A,BandC are in a swimming race. AandB have the same probability of winning and each is twice as likely to win as C. Find the probability that the BorC wins. Assume no two reach the winning point simultaneously.
View SolutionFor a post,three persons A, B and C appearin the interview. The probability of A being selected is twice that of B and the probability of b being selected is thrice that of C. What of the individual probability of A, B and C being selected?
View Solution
Knowledge Check
Identify the parts labelled as A, B, C, D and E in the given diagram of a human sperm and select the correct option.
 AA-Nucleus, B-Tail, C-Mitochondria,
AA-Nucleus, B-Tail, C-Mitochondria,
D-Acrosome, E-CentrioleBA-Acrosome, B-Nucleus,
C-Centriole, D-Mitochondria,
E-Plasma membraneCA-Nucleus, B-Mitochondria,
C-Plasma membrane,
D-Centriole, E-NeckDA-Acrosome, B-Centriole,
C-Mitochondria, B-Centriole,
C-Mitochondria, D-Plasma membrane, E-TailGiven is the diagrammatic sketch of a certain type of connective tissue
Identify the parts labelled as A,B,C and D and select the correct option.
 A A B C D Macrophage Fibroblast Collagen fibres Mast cellB A B C D Mast cell Macrophage Fibroblast Collagen fibreC A B C D Macrophage Collagen fibre Fibroblast Mast cellD A B C D Mast cell Collagen fibre Fibroblast Macrophage
A A B C D Macrophage Fibroblast Collagen fibres Mast cellB A B C D Mast cell Macrophage Fibroblast Collagen fibreC A B C D Macrophage Collagen fibre Fibroblast Mast cellD A B C D Mast cell Collagen fibre Fibroblast Macrophage
A and B are two candidates seeking admission in a college. The probability that A is selected is 0.7 and the probability that exactly one of them is selected is 0.6. Find the probability that B is selected.
View SolutionIdentify the parts labelled as A, B, C and D in the given ultrastructure of a plant cell and select the correct option.

View SolutionGiven below is the diagram of the transverse section of monocot stem. Identify the parts labelled A, B, C and D and select the right option about the

View SolutionIf A and B are two candidates seeking admission in an engineering college. The probability that A is selected is 0.5 and the probability that both A and B are selected is at most 0.3. Is it possible that the probability of B getting selected is 0.7 ?
View SolutionIdentify the parts labelled as A,B,C and D in the given figure and select the correct option from the given codes.
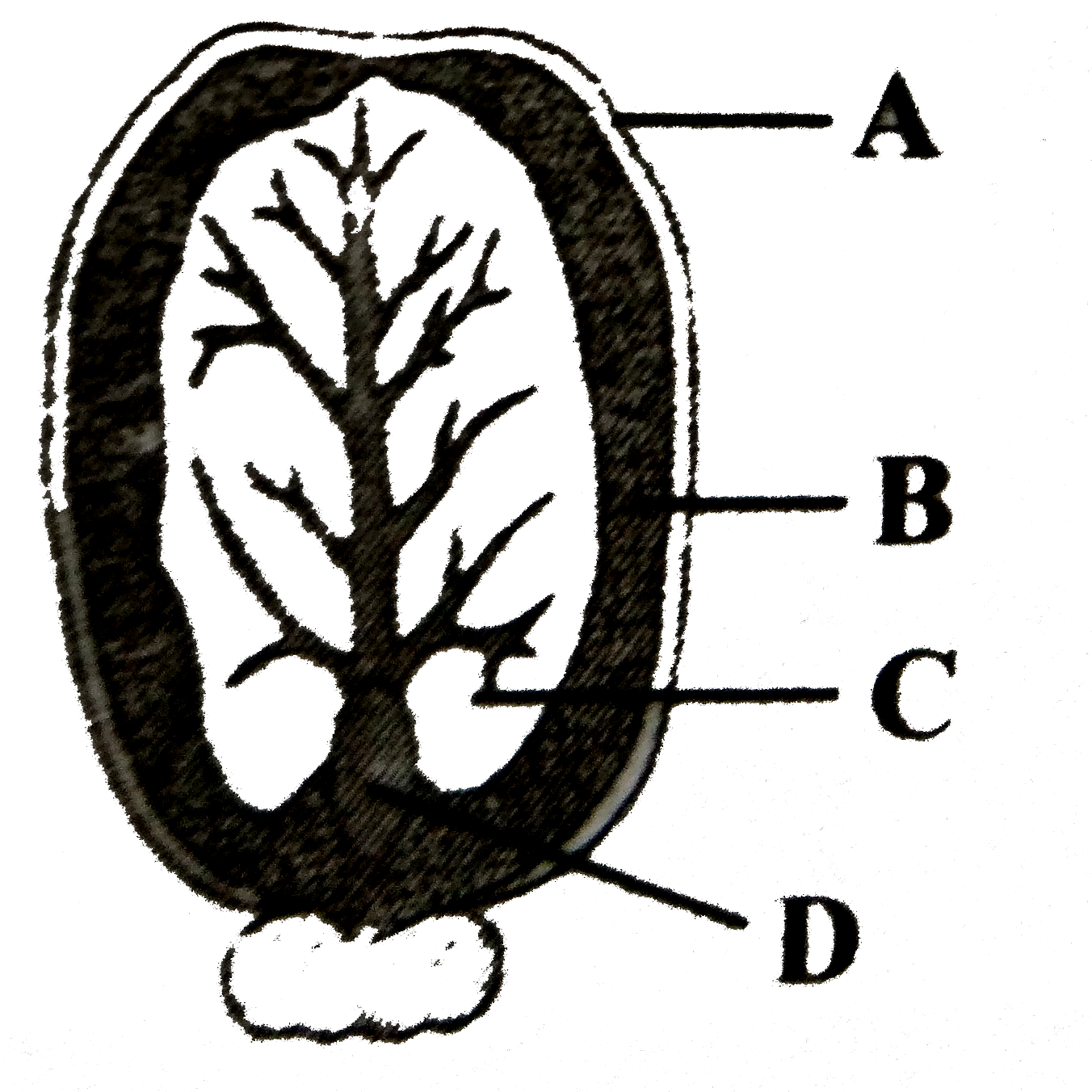
View SolutionGiven is the diagrammatic sketch of a certain type of connective tissue
Identify the parts labelled as A,B,C and D and select the correct option.

View Solution
