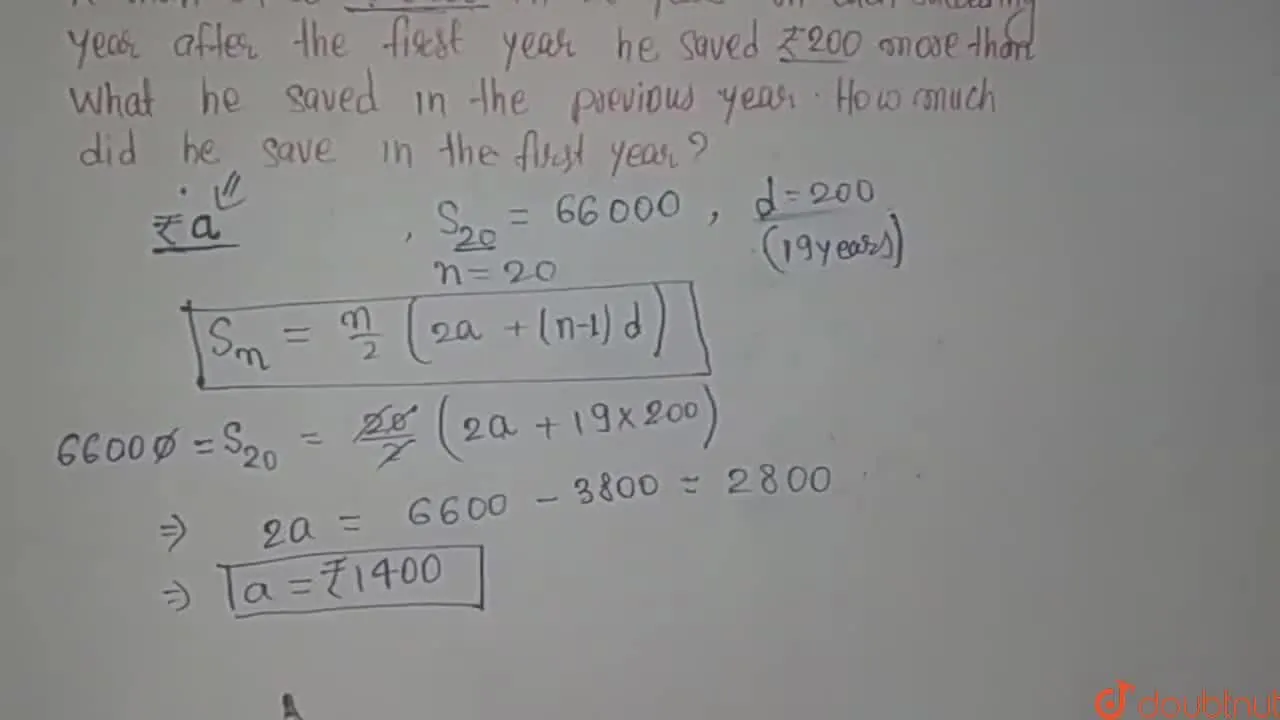A man saved Rs. 66000 in 20 years. In each succeeding year after the first year he saved Rs. 200 more than what he saved in the previous year. How much did he save in the first year?
Let saved in first Rs. Since each succeeding year an ncrement Rs. 200 has made.
So , it forms an AP whose
Fiist term = a common difference (d) - 200 and b-20yr
thererforeS20=202[2a+(20−1)d][∵Sn=n2{2a+(n−1)d}]
⇒660000=10[2a+19d]
⇒66000=20a+190d
⇒66000=20a+190×200
⇒20a=66000−38000
⇒20a=28000
∴a=2800020=1400
hence , he saved Rs. 1400 in the first year.
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - long answer type questions4videos
SEQUENCE AND SERIES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Objective type Question10videos
SEQUENCE AND SERIES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - True /False5videos
RELATIONS AND FUNCTIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SETSEXERCISE - TRUE AND FALSE6videos
SETS
Similar Questions
A man saved Rs. 16500 in ten years. In each year after the first he saved Rs. 100 more than be did in the receding year. How many did he save in the first year?
View SolutionA man saved Rs. 16500 in ten years. In each year after the first he saved Rs. 100 more than be did in the receding year. How many did he save in the first year?
View SolutionA man saved रु 16,500 in 10 years. In each year after the first he saved 100 more than he did in the preceding year. How much did he save in the first year?
View SolutionA man borrows रु 10,000 at 5% per annum compound interest. He repays 35% of the sum borrowed at the end of the first year and 42% of the sum borrowed at the end of the second year. How much must he pay at the end of the third year in order to clear the debt?
View SolutionA man saves Rs. 200 in each of the first three months of his service. In each of the subsequent months his saving increases by Rs. 40 more than the saving of immediately previous month. His total saving from the start of service will be Rs. 11040 after how many months
View SolutionGautam takes a loan of Rs. 16,000 for 2 years at 15% p.a. compound interest. He repays Rs. 9,000 at the end of first year. How much must he pay at the end of second year to clear the debt ?
View SolutionA man saves Rs. 200 in each of the first three months of his service. In each of the subsequent months In each of ther mupienent montha his saving increases by Rs, 40 more than the saving of immediately previous month. His total saving s from the start of service will be Rs. 11040 after
View SolutionA man borrowed Rs. 20,000 for 2 years at 8% per year compound interest. Calculate :
the interest of the second year.View SolutionA man borrowed Rs. 20,000 for 2 years at 8% per year compound interest. Calculate :
the final amount at the end of the second year.View SolutionRohit borrowed Rs. 24,000 at 7⋅5 percent per year. How much money will he pay at the end of 4 years to clear his debt ?
View Solution