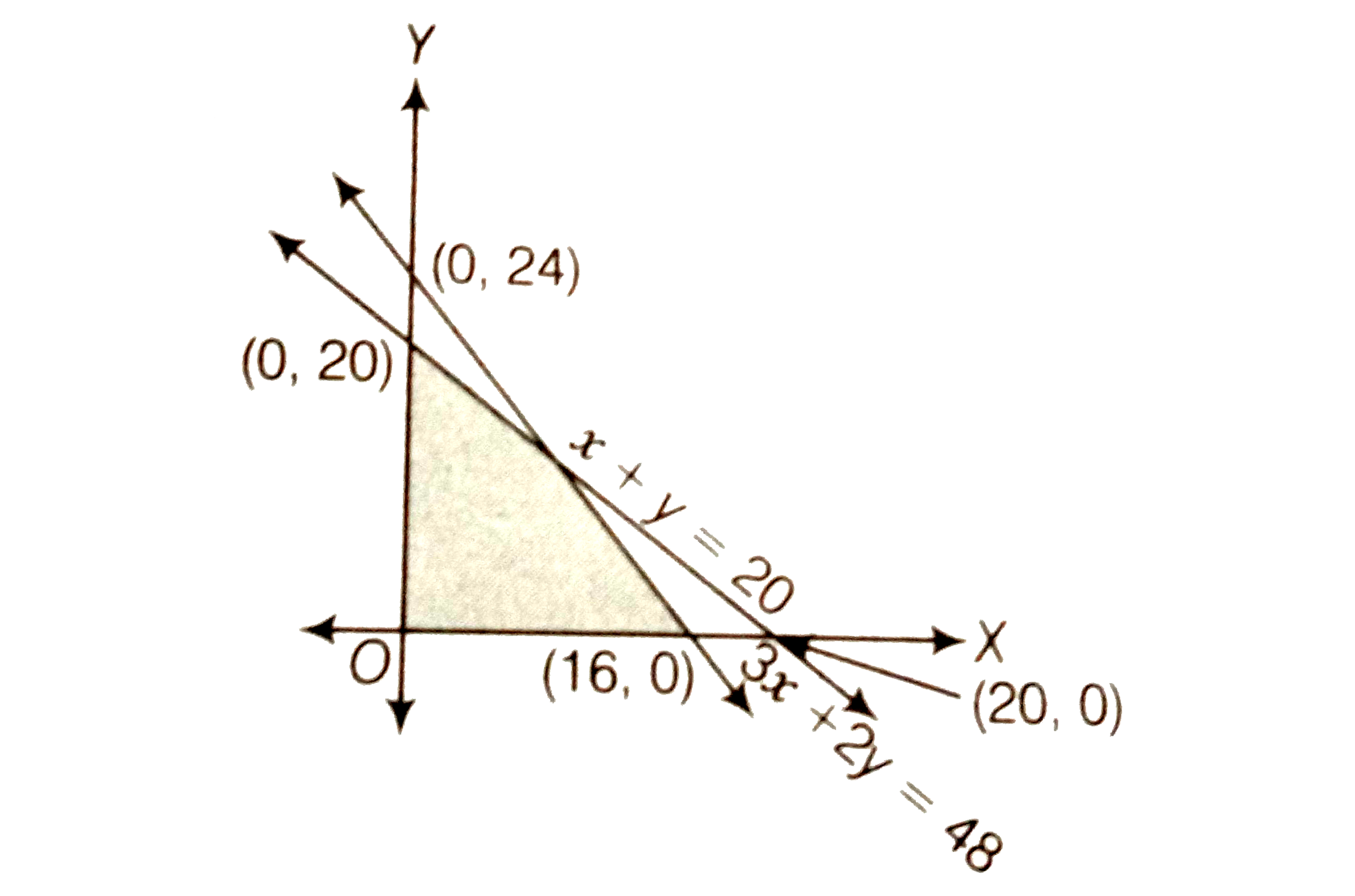
Find the linear inequalities for which the shaded region in the given figure is the solution set.
Video Solution
Text Solution
Consider the line 3x+2y=48, we observe that the shaded and the origin are on the same side of the line 3x+2y=48and(0,0) satisfy the linear constraint 3x+2y≤48. So, we must have one inequation as 3x+2y≤48.
Now, condider the line x+ y = 20 . We find that the shaded region and the origin are on the same side of the line x + y = 20 and (0, 0) satisfy the constraints x+y≤20. So, the second inequation is x+y≤20.
We also notice that the shaded region is above X- axis and is on the right side of y-axis, so we must have x≥0,y≥0.
Thus, the linear inequations corresponding to the given solution set are 3x+2y≤48,x+y≤20andx≥0,y≥0.
|
Topper's Solved these Questions
- LINEAR INEQUALITIESBook:NCERT EXEMPLAR ENGLISHChapter:LINEAR INEQUALITIESExercise:Objective Type Questions
Explore 14 Videos
- LINEAR INEQUALITIESBook:NCERT EXEMPLAR ENGLISHChapter:LINEAR INEQUALITIESExercise:Objective Type Questions
Explore 14 Videos
- LIMITS AND DERIVATIVES Book:NCERT EXEMPLAR ENGLISHChapter:LIMITS AND DERIVATIVES Exercise:FILLERS
Explore 4 Videos
- MATHEMATICAL REASONING Book:NCERT EXEMPLAR ENGLISHChapter:MATHEMATICAL REASONING Exercise:OBJECTIVE TYPE QUESTIONS
Explore 21 Videos
Similar Questions
Knowledge Check
What is the area of shaded region in the figure?
 A10π+27√3B10π+274√3C30π+27√3D30π+9√3
A10π+27√3B10π+274√3C30π+27√3D30π+9√3
Find the linear inequations for which the shaded area in fig. 15.41 is the solution set. Draw the diagram of the solution set of the linear inequations.
View SolutionFind the linear equations for which the shaded area in Fig: 15.39 is the solution set.
View SolutionFind the area of the shaded region in the adjoing figure :
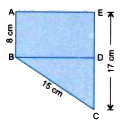
View SolutionFind the area of the shaded region in the adjoing figure :

View SolutionFind the area of the shaded region in the adjoing figure :

View SolutionFind the area of the shaded region in the adjoing figure :
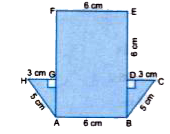
View SolutionFind the area of the shaded region in the adjoing figure :

View Solution

