Out of 100 students 15 passed in English 12 in Mathematics , 8 in Science 6 in English and Mathematics 7 in Mathematics and Science 4 in English and science and 4 in all the three .Find how many students passed
(a) in English and Mathmatics but not in science
( b) in Mathematics and science but not in English
(c) in Mathematics only
(d) in more than one subujects
Let M be the set of students who passed in Mathematics, E be the set of students who passed in English and S be the set of students who passed in Science.
Then, n(u)=100,
n(E)=15,n(M)=12,n(S)=8,n(E∩M)=6,n(M∩S)=7,
n(E∩S)=4, and n(E∩M∩S)=4.
∴n(E)=15
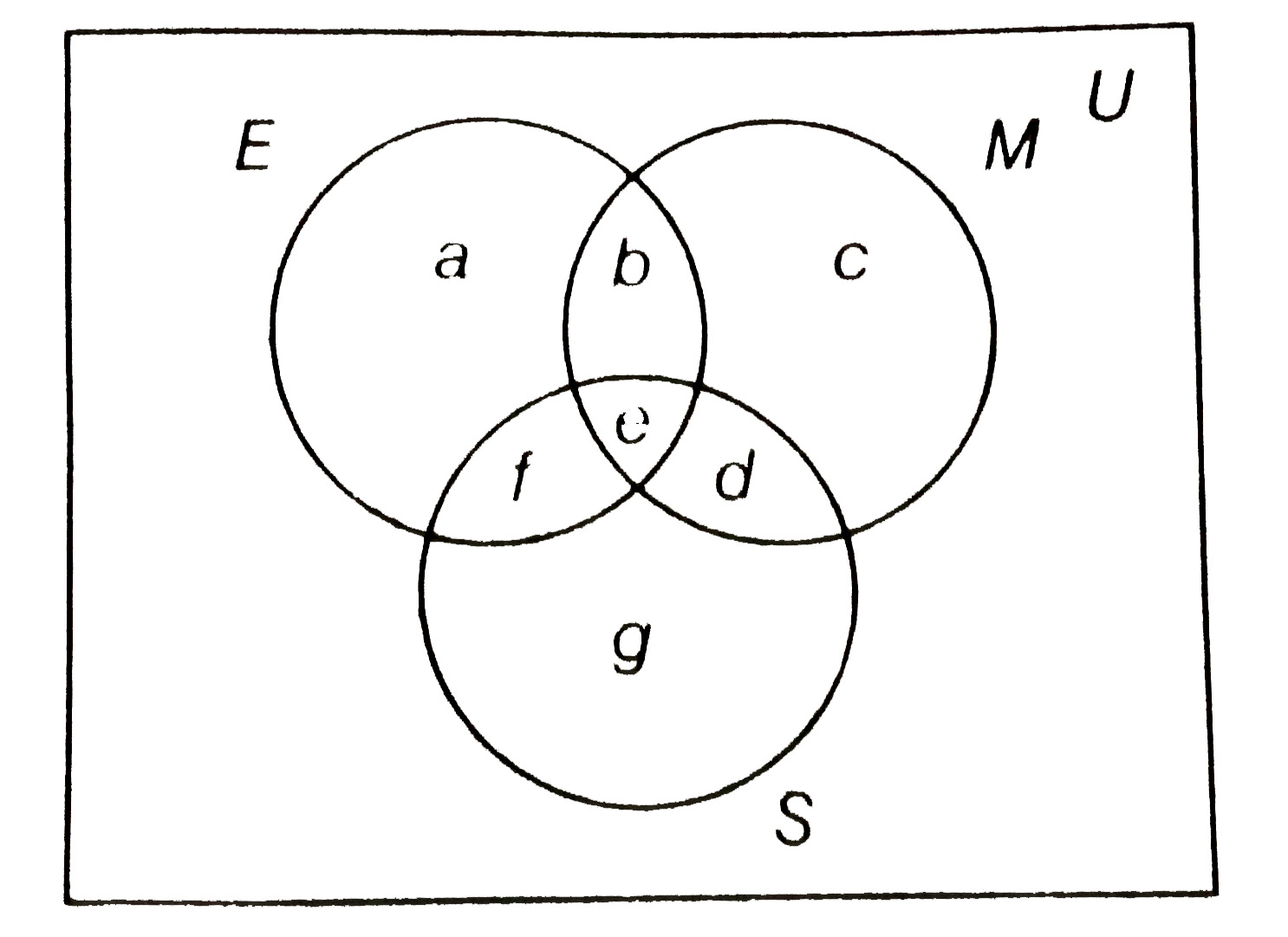
⇒a+b+e+f=15.....(i)
and n(M)=12
⇒b+c+e+d=12.....(ii)
Also, n(S)=8
⇒d+e+f+g=8.......(iii)
n(E∩M)=6
⇒b+e=6.......(iv)
n(M∩S)=7
⇒e+d=7......(v)
n(E∩S)=4
⇒e+f=4.......(vi)
n(E∩M∩S)=4
⇒e=4.......(vii)
From Eqs. (vi) and (vii), f=0
From Eqs. (v) and (vii). d=3
From Eqs. (iv) and (vii). b=2
On substiuting the values of d, e and f in Eq. (iii), we get
3+4+0+g=8
⇒g=1
On substituting the value of b, e and d in Eq. (ii) we, get
2+c+4+3=12
⇒c=3
On substituting b, e, and f in Eq. (i), we get
a+2+4+0=15
⇒a=9
(i) Number of students who passed in English and Mathematics but not in Science
=b=2
(ii) Number of students who passed in Mathematics and Science but not in English
=d=3
(iii) Number of students who passed in Mathematics only =c=3
(iv) Number of students who passed in more than one subject
=b+e+d+f
=2+4+3+0=9
Alternate Method
Let E denote the set of student who passed in English. M denotes the set of students who passed in Mathematics. S denotes the set of students who passed in Science.
Now, n(U)=100,n(E)=15,n(m)=12,n(S)=8,
n(E∩M)=6,n(M∩S)=7,
n(E∩S)=4,n(E∩M∩S)=4
(i) Number of students passed in English and Mathematics but not in Science
i.e., n(E∩M∩S')=n(E∩M)−n(E∩M∩S),[∵A∩B'=A−(A∩B)]
=6−4=2
(ii) Number of students passed in Mathematics and Science but not in English.
i.e. n(M∩S∩E')=n(M∩S)−n(M∩S∩E)
=7−4=3
(iii) Number of students passed in mathematics only
i.e., n(M∩S'∩E')=n(M)−n(M∩S)−n(M∩E)+(M∩S∩E)
=12−7−6+4=3
(iv) Number of students passed in more than one subjected only
i.e., n(E∩M)+n(M∩S)+n(E∩S)−3n(E∩M∩S)+n(E∩M∩S)
=6+7+4−4×3+4
=17−12+4=5+4=9
Topper's Solved these Questions
- SETSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SETSEXERCISE - OBJECTIVE TYPE QUESTIONS
14 Videos
- SETSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SETSEXERCISE - FILLERS
9 Videos
- SETSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SETSEXERCISE - TRUE AND FALSE
6 Videos
- SEQUENCE AND SERIESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Match the comumms
2 Videos
- STATISTICSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICSEXERCISE - FILLERS
7 Videos
Similar Questions
Out of 100 students, 15 passed in English, 12 passed in Mathmatics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science , 4 in English and Science, 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science.
(ii) in Mathematics and Science but not in English.
(iii) in Mathematics only.
(iv) in more than one subject only.
View SolutionScience of algae is
View Solution
Knowledge Check
Raza scored 30 marks in Maths, x marks in Science and y marks in English. What is his total score in these three subjects ?
A30+x+yB30+x−yCx+y−30D30+30x+30y
Sunny scored x marks in Maths, y marks in Science and 50 marks in English. What is his total score in these three subjects?
View SolutionClimatology is science of
View SolutionThere are five books on Mathematics and 6 books on Physics in a book shop. In how many ways can a student buy : (i) a Mathematics book and a Physics book (ii) either a Mathematics book or a Physics book?
View SolutionAnjali scores 100 marks in Mathematics and x marks in Science. what is her total score in Science and Mathematics?
View SolutionThe marks obtained by 10 candidates in English and Mathematics are given below:
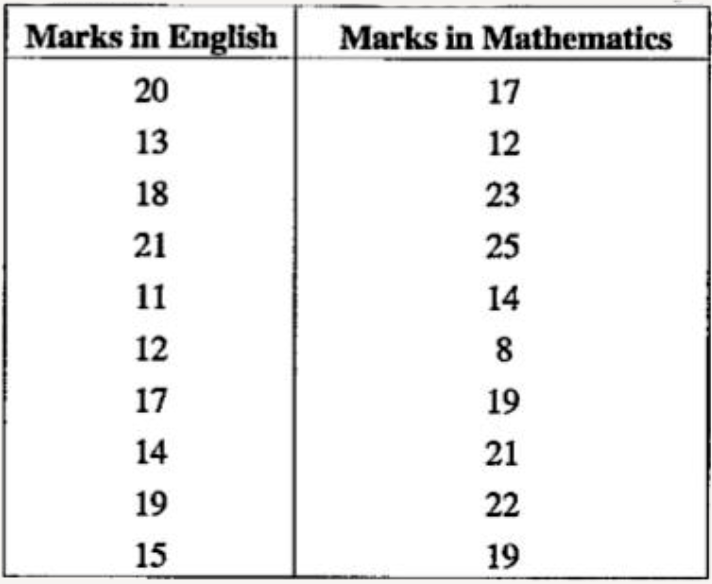
Estimate the probable score for Mathematics if the marks obtained in English are 24.
View SolutionSaina secure 70 marks in Science and 80 marks in Mathematics. Find
a. the ratio of Sania's marks in Science to her marks in Mathematics.
b. the ratio of Sania's marks in Mathematics to her marks is Science.
View Solution72% of 25 students are good in mathematics. How many are not good in mathematics?
View Solution
