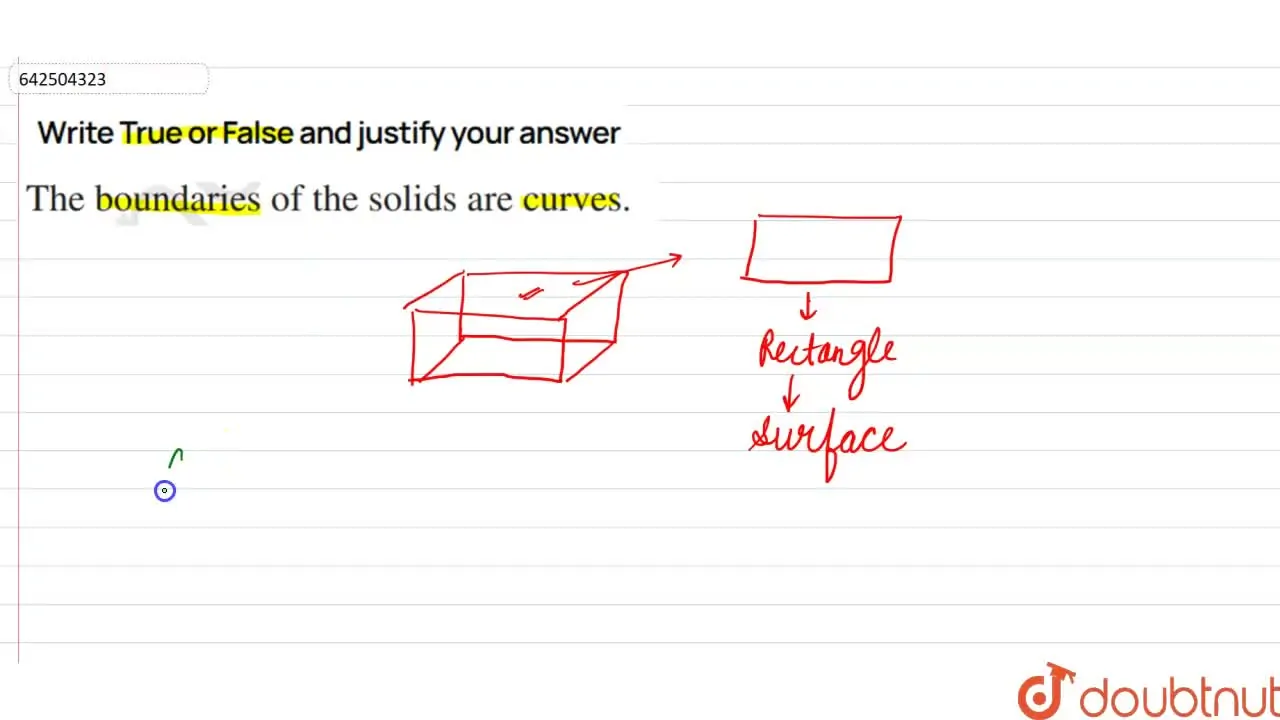
The boundaries of the solids are curves.
Because the boundaries of the solids are surfaces.
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO EUCLID GEOMETRYEXERCISE - Exercise 5.3 Short Answer Type Questions12videos
INTRODUCTION TO EUCLID GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO EUCLID GEOMETRYEXERCISE - Exercise 5.4 Long Answer Type Questions5videos
INTRODUCTION TO EUCLID GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO EUCLID GEOMETRYEXERCISE - Exercise 5.4 Long Answer Type Questions5videos
INTRODUCTION TO EUCLID GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - HERON'S FORMULAEXERCISE - Long Answer Type Questions8videos
HERON'S FORMULA
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR EQUATION IN TWO VARIABLESEXERCISE - Exercise 4.81videos
LINEAR EQUATION IN TWO VARIABLES
Similar Questions
Boundaries of solids are
View SolutionBoundaries of surfaces are curves.
View SolutionThe area of the region whose boundaries are defined by the curves y=2 cos x, y=3 tan x, and the y-axis is
View SolutionThe boundary of the shaded region in the given figure consists of three semicircular areas, the smaller ones being equal. If the diameter of the larger one is 14 cm, calculate
(i) the length of the boundary
(ii) the area of the shaded regionView SolutionThe boundaries of which of the following kingdom is not well defined ?
View SolutionA solid cone of height H and base radius H2 floats in a liquid of density ρ. It is hanging from the ceiling with the help of a string. The force by the fluid on the curved surface of the cone is (P0= atmospheric pressure)
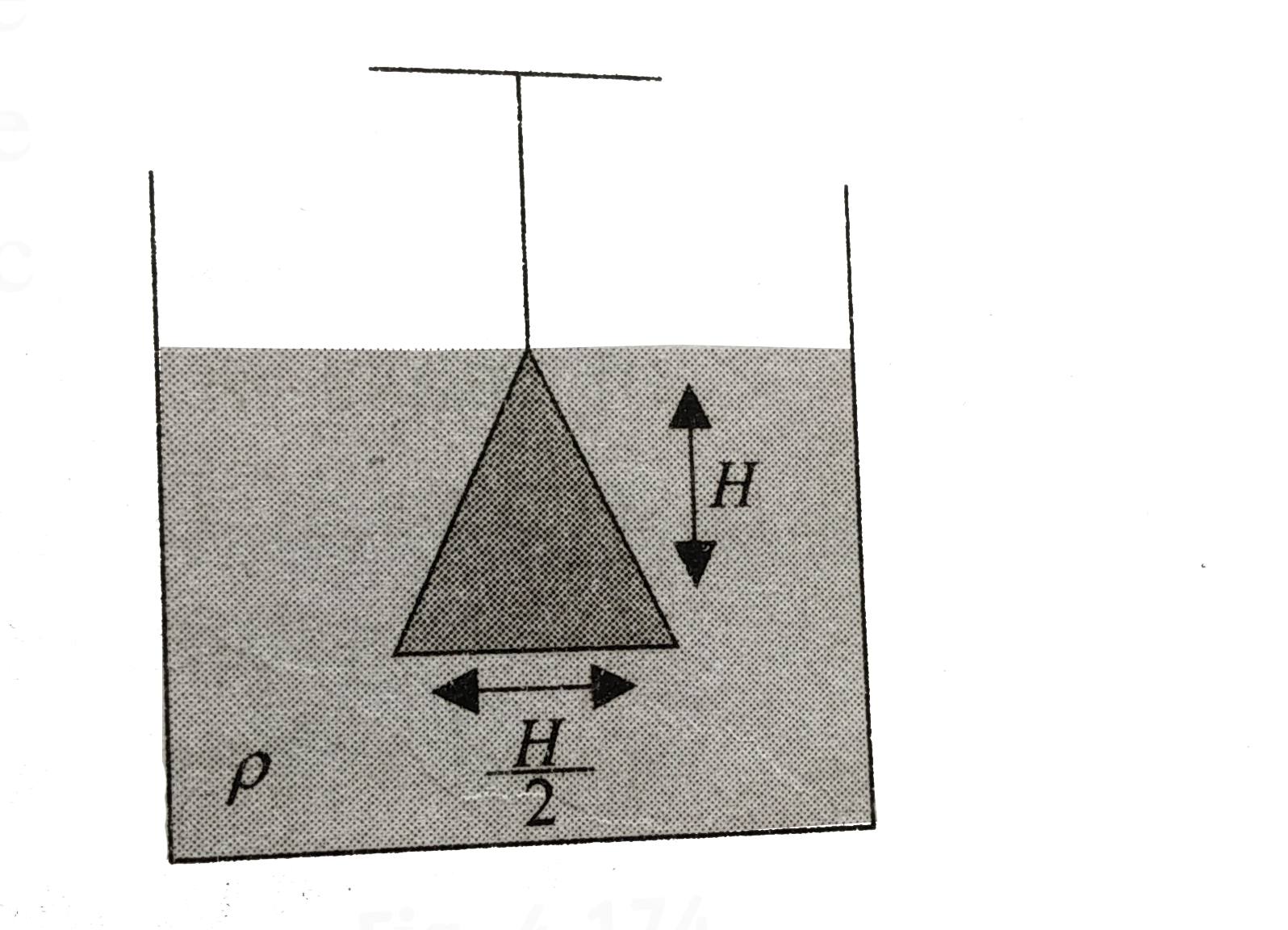 View Solution
View SolutionA right triangle with sides 6 cm, 8 cm and 10 cm is revolved about the side 8 cm. Find the volume and the curved surface of the solid so formed.
View SolutionName the methods of separation of the components of solid-solid mixtures.
View SolutionAre plasma membranes the outer boundaries of all cells? Explain.
View SolutionThe radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its :
curved surface areaView Solution