Plot the points A(1,-1) and B(4,5).
(i) Draw the line segment joining these points. Write the coordinates of a point on this line segment between the points A and B.
(ii) Extend this line segment and write the coordinates of a point on this line which lies outside the line segment AB.
To solve the problem step by step, we will follow the instructions provided in the question.
Step 1: Plot the Points A and B
We need to plot the points A(1, -1) and B(4, 5) on a Cartesian plane.
- Point A has coordinates (1, -1). This means we move 1 unit to the right on the x-axis and 1 unit down on the y-axis.
- Point B has coordinates (4, 5). This means we move 4 units to the right on the x-axis and 5 units up on the y-axis.
Step 2: Draw the Line Segment Joining A and B
Now that we have plotted both points, we will draw a straight line segment connecting points A and B.
Step 3: Find a Point on the Line Segment AB
To find a point on the line segment between A and B, we can take the midpoint or any point that lies between the two coordinates.
Let's calculate the midpoint:
- Midpoint M = (x1+x22,y1+y22)
- Here, x1=1, y1=−1, x2=4, y2=5.
Calculating:
- M=(1+42,−1+52)=(52,42)=(2.5,2)
So, the coordinates of a point on the line segment AB are (2.5, 2).
Step 4: Extend the Line Segment AB
To extend the line segment AB, we can continue the line in either direction. We will find a point that lies outside the segment AB.
Let's choose a value for x that is greater than the x-coordinate of point B (which is 4). We can choose x=6.
Step 5: Find the Corresponding y-coordinate
Using the slope-intercept form of the line equation derived from points A and B, we can find the y-coordinate.
1. Find the slope (m):
- Slope m=y2−y1x2−x1=5−(−1)4−1=63=2
2. Use point-slope form to find the equation of the line:
- The equation of the line can be written as:
y−y1=m(x−x1)
- Using point A(1, -1):
y+1=2(x−1)
- Rearranging gives:
y=2x−3
3. Substituting x = 6 into the equation:
y=2(6)−3=12−3=9
Thus, the coordinates of a point on the extended line that lies outside the line segment AB are (6, 9).
Summary of Results
- A point on the line segment AB: (2.5, 2)
- A point on the extended line outside AB: (6, 9)
We need to plot the points A(1, -1) and B(4, 5) on a Cartesian plane.
- Point B has coordinates (4, 5). This means we move 4 units to the right on the x-axis and 5 units up on the y-axis.
Now that we have plotted both points, we will draw a straight line segment connecting points A and B.
To find a point on the line segment between A and B, we can take the midpoint or any point that lies between the two coordinates.
- Midpoint M = (x1+x22,y1+y22)
- Here, x1=1, y1=−1, x2=4, y2=5.
- M=(1+42,−1+52)=(52,42)=(2.5,2)
To extend the line segment AB, we can continue the line in either direction. We will find a point that lies outside the segment AB.
Using the slope-intercept form of the line equation derived from points A and B, we can find the y-coordinate.
- Slope m=y2−y1x2−x1=5−(−1)4−1=63=2
- The equation of the line can be written as:
y−y1=m(x−x1)
- Using point A(1, -1):
y+1=2(x−1)
- Rearranging gives:
y=2x−3
y=2(6)−3=12−3=9
- A point on the line segment AB: (2.5, 2)
- A point on the extended line outside AB: (6, 9)
Topper's Solved these Questions
- COORDINATE GEOMETRYBook:NCERT EXEMPLAR ENGLISHChapter:COORDINATE GEOMETRYExercise:Exercise 3.3 Short Answer Type Questions
Explore 12 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Long Answer Type Questions
Explore 5 Videos
- HERON'S FORMULABook:NCERT EXEMPLAR ENGLISHChapter:HERON'S FORMULAExercise:Long Answer Type Questions
Explore 8 Videos
Similar Questions
Knowledge Check
If point C(−4,1) divides the line segment joining the point A(2,−2) and B in the ratio 3:5, then the coordinates of B are
A(a) (−14,6)B(b) (6,−14)C(c) (−14,−6)D(d) (−6,−14)
Find the coordinates of the points which trisect the line segment joining the points (2,3)and(6,5).
View SolutionThe point P(-4,2) lies on the line segment joining the points A(-4,6) and B (-4,-6).
View SolutionFind the co-ordinates of the points of trisection of the line segment joining the points A(−5,6)andB(4,−3).
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
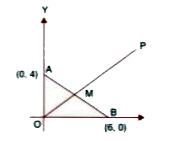
co-ordinates of P
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
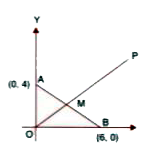
co-ordinates of M
View SolutionIn what ratio is the line segment joining the points A(-2, -3) and B(3, 7) divided by the y-axis? Also, find the coordinates of the point of division.
View SolutionWrite the coordinates of the point dividing line segment joining points (2, 3) and (3, 4) internally in the ratio 1 :5 .
View Solution

