An automobile engine propels a 1000 kg car (A) along a levelled road at a speed of 36 km//h. Find the power if the opposing frictional force is 100 N Now, suppose after travelling a distance of 200 m, this car collides with another stationary car (B) of same mass and comes to rest. Let its engine also stop at the same time. Now car (B) starts moving on the same level road without getting its engine started. Find the speed of the car (B) just after the collision.
Given, mass of car (A) = 1000kg
Mass of car B = 1000kg
Force applied by car A = 100 N
(vA)Speed of car(A)=36kmh−1=36×518=10ms−1[∵1km/h=518m/s]
∴Power of car(A),PA=F.vA=100×10=1000W
[F=force exerted by the car underset(-)A against friction]
Again, for car (A) Newton's low, F = ma
100=1000×a⇒a=1001000
a=110ms−1
Velocity of car A after travelling 200 m is given by
From third equatioin of motion, v2=u2+2as [for c ar A here,u=10ms−1,s=200m]
v2=(10)2+2×110×200
v2=100+40=140
v=√140=11.8ms−1
According to the question, after moving of 200m, the speed of car A, u1=11.8ms−1
Just after the collision, the final speed of car A, v1=0
before collision, the initial speed of car B, u2=0
From conservation of linear momentum,
m1u1+m2u2=m1v1+m2v2
[Let just after the after the collision, the speed of the car B is v2]
m1×11.8m1+m2×0=m1×0+m2×v2
11.8m1=m2v2 [As∵m1=m2]
11.8m1=m1v2
⇒v2=11.8ms−1
Topper's Solved these Questions
Similar Questions
Knowledge Check
A car moving along a straight road with speed of 144kmh−1 is brought to a stop within a distance of 200 m. How long does it take for the car to stop ?
A5 sB10 sC15 sD20 sA car travelling at a speed of 30 km per hour is brought to rest in 8 metres by applying brakes. If the same car is travelling at 60 km per hour, it can be brought tor est with the same braking force at a distance of
A16 mB24 mC32 mD36 mThe distance between station A and B by road is 240 km and by train it is 300 km. A car starts from station A with a speed : km/hr whereas a train starts from station B with a speed 20 km/hr more than the speed of the car.
The speed of the car is:A60 km/hrB120 km/hrC40 km/hrD80 km/hr
A rail road car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man aproaching the engine?
View SolutionA car travelling with a speed 125 KMPH along a straight line comes to rest after travelling a distance 245 m.The time taken by the car to come to rest,in second is
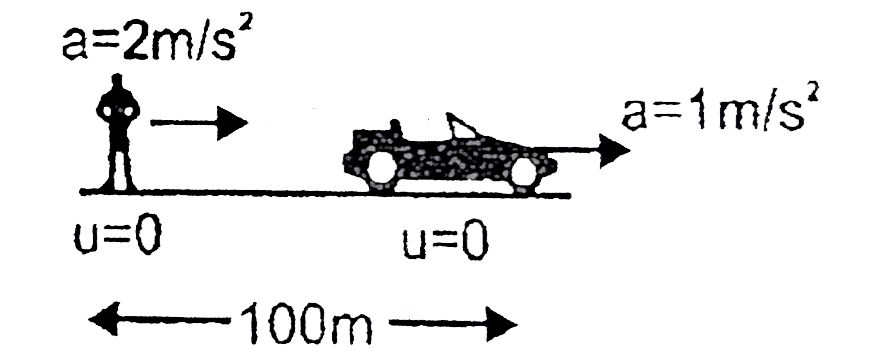
View SolutionInitially a man and a car both are stationary and situated at a distance of 100m. Now both starts moving simltaneously in the same direction as shown in figure. Then :
View SolutionA car having a mass of 1000 kg is moving at a seed of 30 metres/sec. Brakes are applied to bring the car to rest if the frictional force between the tyres and the road surface is 5000 newtons,the car will come to reast in
View SolutionA car runs east to west and another car B of the same mass runs from west to east at the same path along the equator. A presses the track with a force N1 and B presses the track with a force N2. Then
View Solution
