Area under graph represents a physical quantity which has the unit
m
To determine the physical quantity represented by the area under a velocity-time (v-t) graph, we can follow these steps:
1. Understanding the Graph:
- A velocity-time graph plots velocity (v) on the y-axis and time (t) on the x-axis.
2. Identifying the Area:
- The area under the v-t graph represents the product of velocity and time. This can be expressed mathematically as:
Area=∫vdt
- This integral calculates the area under the curve, which is essentially the sum of small rectangles formed by the velocity at each instant multiplied by the time interval.
3. Calculating the Area:
- The area can also be interpreted as:
Area=v×t
- Here, v is the velocity (in meters per second, m/s) and t is the time (in seconds, s).
4. Determining the Units:
- The unit of velocity is meters per second (m/s).
- The unit of time is seconds (s).
- Therefore, when we multiply these units:
Units of Area=(m/s)×s=m
- This shows that the area under the v-t graph has the unit of meters (m).
5. Conclusion:
- The area under the v-t graph represents the physical quantity of distance or displacement, which is measured in meters.
Final Answer:
The area under the velocity-time graph represents a physical quantity which has the unit of meters (m).
---
- A velocity-time graph plots velocity (v) on the y-axis and time (t) on the x-axis.
- The area under the v-t graph represents the product of velocity and time. This can be expressed mathematically as:
Area=∫vdt
- This integral calculates the area under the curve, which is essentially the sum of small rectangles formed by the velocity at each instant multiplied by the time interval.
- The area can also be interpreted as:
Area=v×t
- Here, v is the velocity (in meters per second, m/s) and t is the time (in seconds, s).
- The unit of velocity is meters per second (m/s).
- The unit of time is seconds (s).
- Therefore, when we multiply these units:
Units of Area=(m/s)×s=m
- This shows that the area under the v-t graph has the unit of meters (m).
- The area under the v-t graph represents the physical quantity of distance or displacement, which is measured in meters.
The area under the velocity-time graph represents a physical quantity which has the unit of meters (m).
Topper's Solved these Questions
- MOTIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOTIONEXERCISE - Short Answer Type Questions
7 Videos
- MOTIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOTIONEXERCISE - Long Answer Type Questions
6 Videos
- GRAVITATIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GRAVITATIONEXERCISE - LONG ANSWER TYPE QUESTIONS
4 Videos
- SOUNDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SOUNDEXERCISE - Long Answer Type Questions
3 Videos
Similar Questions
A physical quantity which has a direction:-
View SolutionA physical quantity which has a direction:-
View SolutionName a derived physical quantity with its Sl unit.
View SolutionGive an example of (a) a physical quantiy which has a unit but no dimensions. (b) a physical quantity which has neither unit no dimensions. (c ) a constant which has a unit. (d) a constant which has no unit.
View SolutionThe physical quantity that has no dimensions is
View SolutionMatch the following physical quantities with units.
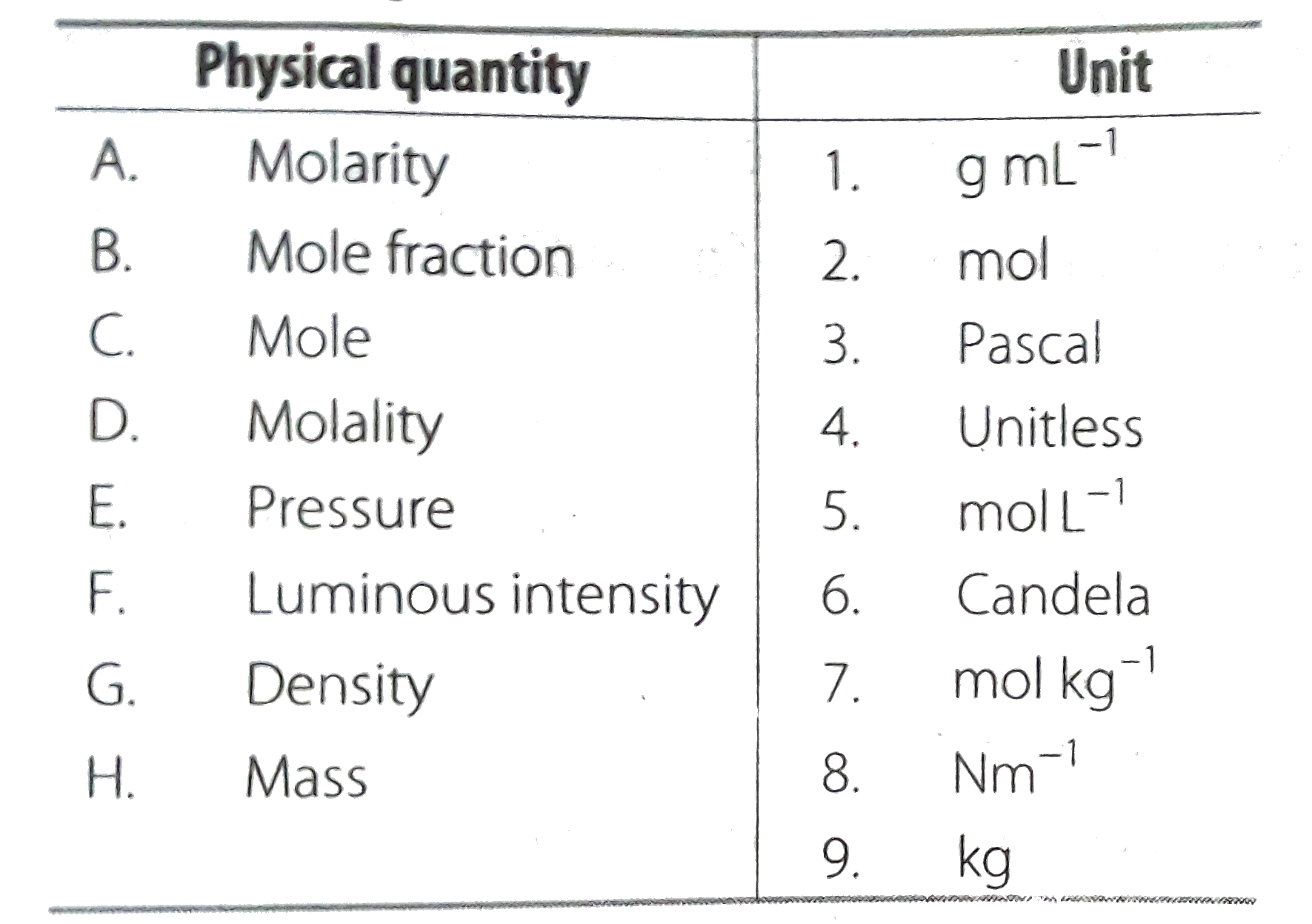
View SolutionName a physical quantity related to the unit light year
View SolutionWeber is the unit of which physical quantity?
View SolutionName the physical quantities which are measured in the following unit
ns
View SolutionName the physical quantities which are measured in the following unit
u
View Solution
