If a proton had a radius R and the charge was uniformaly fistributed , Calculate using bohr theory, the ground state energy of a H-atom When R=10Å
To calculate the ground state energy of a hydrogen atom using Bohr's theory when the radius of the proton is given as R=10Å, we can follow these steps:
Step 1: Understand the formula for energy
The energy E of the electron in a hydrogen atom is given by the formula:
E=−Ze28πϵ0r
where:
- Z is the atomic number (for hydrogen, Z=1),
- e is the charge of the electron (e=1.6×10−19C),
- ϵ0 is the permittivity of free space (ϵ0=8.854×10−12C2/N m2),
- r is the radius of the orbit (in this case, R=10Å=10×10−10m).
Step 2: Substitute the values into the formula
Substituting the known values into the energy formula:
E=−1⋅(1.6×10−19)28π(8.854×10−12)(10×10−10)
Step 3: Calculate the numerator
Calculate the numerator:
(1.6×10−19)2=2.56×10−38C2
Step 4: Calculate the denominator
Calculate the denominator:
8π(8.854×10−12)(10×10−10)=8⋅3.1416⋅8.854×10−12⋅10×10−10
=8⋅3.1416⋅8.854×10−21≈2.48×10−20C2/N m2
Step 5: Calculate the energy
Now substituting the values back into the energy formula:
E=−2.56×10−382.48×10−20≈−1.03×10−18J
Step 6: Convert energy to electron volts
To convert the energy from joules to electron volts, use the conversion factor 1eV=1.6×10−19J:
E (in eV)=−1.03×10−181.6×10−19≈−6.44eV
Final Answer
The ground state energy of the hydrogen atom when the proton has a radius of R=10Å is approximately:
E≈−6.44eV
The energy E of the electron in a hydrogen atom is given by the formula:
E=−Ze28πϵ0r
where:
- Z is the atomic number (for hydrogen, Z=1),
- e is the charge of the electron (e=1.6×10−19C),
- ϵ0 is the permittivity of free space (ϵ0=8.854×10−12C2/N m2),
- r is the radius of the orbit (in this case, R=10Å=10×10−10m).
Substituting the known values into the energy formula:
E=−1⋅(1.6×10−19)28π(8.854×10−12)(10×10−10)
Calculate the numerator:
(1.6×10−19)2=2.56×10−38C2
Calculate the denominator:
8π(8.854×10−12)(10×10−10)=8⋅3.1416⋅8.854×10−12⋅10×10−10
=8⋅3.1416⋅8.854×10−21≈2.48×10−20C2/N m2
Now substituting the values back into the energy formula:
E=−2.56×10−382.48×10−20≈−1.03×10−18J
To convert the energy from joules to electron volts, use the conversion factor 1eV=1.6×10−19J:
E (in eV)=−1.03×10−181.6×10−19≈−6.44eV
The ground state energy of the hydrogen atom when the proton has a radius of R=10Å is approximately:
E≈−6.44eV
Topper's Solved these Questions
- ATOMSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ATOMSEXERCISE - Short Answer Type
5 Videos
- ALTERNATING CURRENTBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Long Answe types Questions
5 Videos
- COMMUNICATION SYSTEMBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
if we assume only gravitational attraction between proton and electron in hydrogen atom and the Bohr quantizaton rule to be followed, then the expression for the ground state energy of the atom will be (the mass of proton is M and that of electron is m.)
View SolutionAssume that there is no repulsive force between the electrons in an atom but the force between positive and negative charges is given by Coulomb's law as usual . Under such circumtences, calculate the ground state energy of a He-atom.
View Solution
Knowledge Check
If a proton had a radius R and the charge was uniformly distributed, the ground state energy (in eV) of a H -atom for R=0.1Å is
A−13.6B−27.2C−3.4D−30.8The Bohr model for the H-atom relies on the Coulomb's law of electrostatics . Coulomb's law has not directly been varified for very short distances of the order of angstroms. Suppos-ing Coulomb's law between two oppsite charge +q1,−q2 is modified to ∣∣→F∣∣=q1q2(4πε0)r21r2,r≥R0
=q1q2(4πε0)r21R20(R0r)ε,r≤R0
Calculate in such a case , the ground state enenergy of H-atom , if ε=0.1,R0=1ÅA−11.4B−17.3C5.9D−23.2Positronium is just like a H-atom with the proton replaced by the positively charged anti-particle of the electron (called the positron which is as massive as the electron). What would be the ground state energy of positronium ?
A3.4eVB−5.2eVC−6.8eVD−10.2eV
Consider the hydrogen atom to be a proton embededded in a cavity of radius (Bohr radius) whose charge is neutralised by the addition of an electron to the cavity in a vacuum initially slowly .Estimate the average total energy of an electron in to ground state .Also if the magnitude of the average kinetic energy is half of the magnitude of the average energy ,find the average potential energy
View SolutionFigure shows a hemisphere of charge Q and radius R and a sphere of charge 2Q and radius R. The total potential energy of hemisphere is UH and that of the sphere is Us Then.
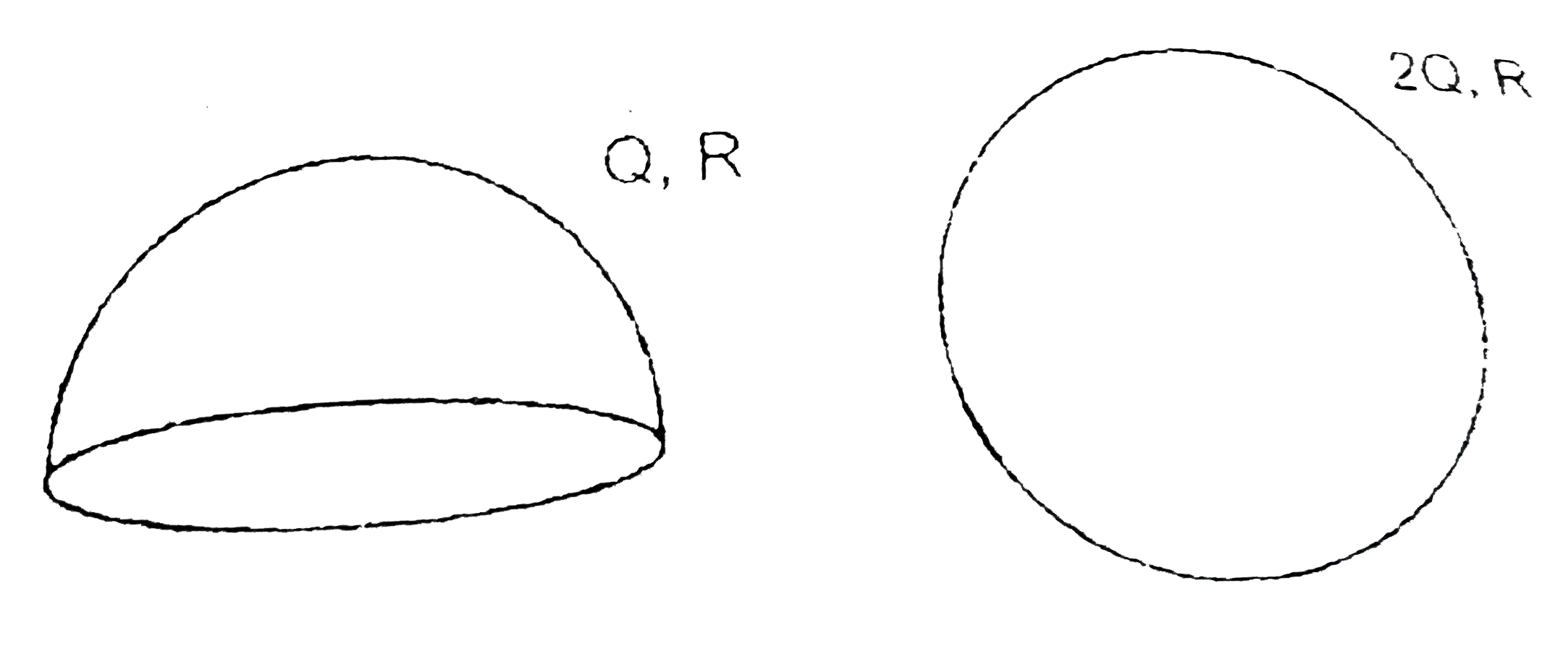
View SolutionA μ−meson("charge -e , mass = 207 m, where m is mass of electron") can be captured by a proton to form a hydrogen - like ''mesic'' atom. Calculate the radius of the first Bohr orbit , the binding energy and the wavelength of the line in the Lyman series for such an atom. The mass of the proton is 1836 times the mass of the electron. The radius of the first Bohr orbit and the binding energy of hydrogen are 0.529Å and 13.6eV , repectively. TakeR = 1.67 xx 109678 cm^(-1)
View SolutionThe ionization energy of a hydrogen like Bohr atom is 4 Rydberg. If the wavelength of radiation emitted when the electron jumps from the first excited state to the ground state is N−m and if the radius of the first orbit of this atom is r−m then the value of Nr=P×102 then, value of P. (Bohr radius of hydrogen =5×10−11m,1 Rydberg =2.2×10−18J)
View SolutionPositronium is just like a H-atom with the proton replaced by the positively charged anti-particle of the electron (called the positron which is as massive as the electron). What would be the ground state energy of positronium ?
View Solution
