Graphically show the total work done in an expansion when the state of an ideal gas is changed reversibly and isothermally from (pi,Vi) to (pf,Vf). With the help of a pV plot compare the work done in the above case with that carried out against a constant pressure pf.
To solve the problem of graphically showing the total work done in an expansion of an ideal gas that changes reversibly and isothermally from (pi,Vi) to (pf,Vf), we will follow these steps:
Step 1: Draw the p-V Diagram
1. Set up the axes: Draw a Cartesian coordinate system where the y-axis represents pressure (P) and the x-axis represents volume (V).
2. Plot the isothermal curve: Since the process is isothermal for an ideal gas, the curve will be a rectangular hyperbola. This curve represents the relationship between pressure and volume for an ideal gas at constant temperature.
Step 2: Mark Initial and Final States
1. Identify the initial and final states: Mark the initial state (pi,Vi) on the curve and the final state (pf,Vf). Ensure that Vi<Vf since it is an expansion.
2. Label the points: Clearly label the points on the curve as A(pi,Vi) and B(pf,Vf).
Step 3: Calculate the Work Done
1. Work done in the process: The work done W during the expansion can be represented as the area under the curve from Vi to Vf.
2. Shade the area: Shade the area under the curve between the two points A and B. This shaded area represents the total work done during the isothermal expansion.
Step 4: Compare with Constant Pressure Work
1. Draw a horizontal line for constant pressure: Draw a horizontal line at pf (the final pressure) across the volume range from Vi to Vf.
2. Calculate the work done at constant pressure: The work done against a constant pressure pf is given by the area of the rectangle formed by the constant pressure line and the volume change, which is Wconstant=pf×(Vf−Vi).
3. Shade this area: Shade the area under the constant pressure line from Vi to Vf.
Step 5: Compare the Areas
1. Analyze the areas: Compare the two shaded areas. The area under the isothermal curve (work done during the isothermal expansion) is larger than the area under the constant pressure line (work done at constant pressure).
2. Conclusion: Conclude that the work done during the isothermal expansion is greater than the work done against a constant pressure pf.
Final Summary
- The total work done during the isothermal expansion is represented by the area under the isothermal curve.
- The work done against a constant pressure is represented by a smaller rectangular area.
- Therefore, the work done in the isothermal process is greater than that done at constant pressure.
1. Set up the axes: Draw a Cartesian coordinate system where the y-axis represents pressure (P) and the x-axis represents volume (V).
2. Plot the isothermal curve: Since the process is isothermal for an ideal gas, the curve will be a rectangular hyperbola. This curve represents the relationship between pressure and volume for an ideal gas at constant temperature.
1. Identify the initial and final states: Mark the initial state (pi,Vi) on the curve and the final state (pf,Vf). Ensure that Vi<Vf since it is an expansion.
2. Label the points: Clearly label the points on the curve as A(pi,Vi) and B(pf,Vf).
1. Work done in the process: The work done W during the expansion can be represented as the area under the curve from Vi to Vf.
2. Shade the area: Shade the area under the curve between the two points A and B. This shaded area represents the total work done during the isothermal expansion.
1. Draw a horizontal line for constant pressure: Draw a horizontal line at pf (the final pressure) across the volume range from Vi to Vf.
2. Calculate the work done at constant pressure: The work done against a constant pressure pf is given by the area of the rectangle formed by the constant pressure line and the volume change, which is Wconstant=pf×(Vf−Vi).
3. Shade this area: Shade the area under the constant pressure line from Vi to Vf.
1. Analyze the areas: Compare the two shaded areas. The area under the isothermal curve (work done during the isothermal expansion) is larger than the area under the constant pressure line (work done at constant pressure).
2. Conclusion: Conclude that the work done during the isothermal expansion is greater than the work done against a constant pressure pf.
- The total work done during the isothermal expansion is represented by the area under the isothermal curve.
- The work done against a constant pressure is represented by a smaller rectangular area.
- Therefore, the work done in the isothermal process is greater than that done at constant pressure.
Topper's Solved these Questions
Similar Questions
For a sample of perfect gas when its pressure is changed isothermally from pi to pf , the entropy change is given by
View SolutionA thermodynamic system goes from states (i) P1,V to 2P1,V (ii) P,V1 to P2,V1. Then work done in the two cases is
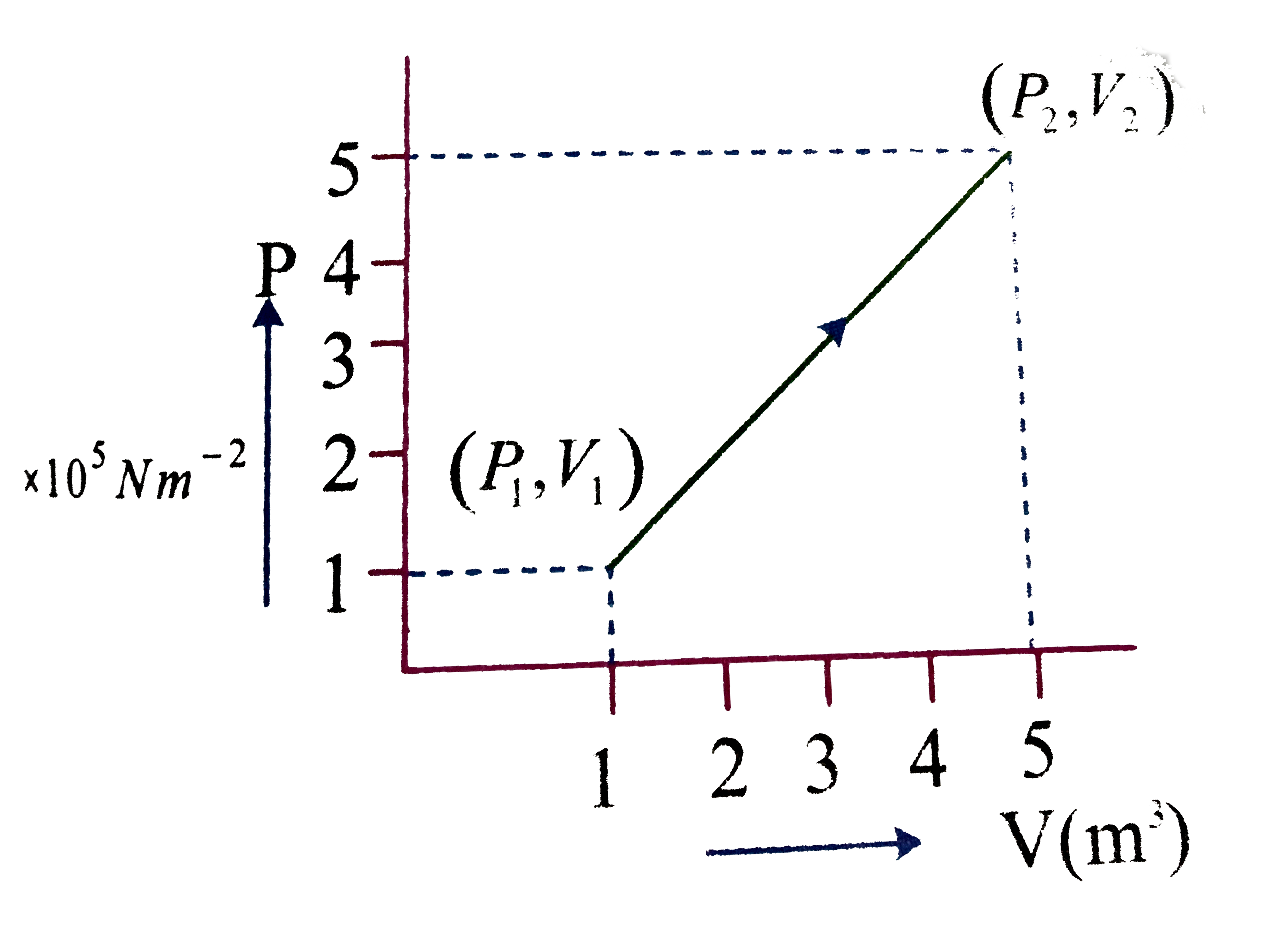
View SolutionA system changes from the state (P1,V1) to (P2,V2) as shown in the diagram. The work done by the system is
View SolutionPressure and volume of a gas changes from (p0V0) to (p04,2V0) in a process pV2= constant. Find work done by the gas in the given process.
View SolutionHow will you calculate work done on an ideal gas in a compression, when change in pressure is carried out in infinite steps ?
View SolutionA sample of an ideal gas with initial pressure 'P' and volume 'V' is taken through an isothermal process during which entropy change is found to be DS. The work done by the gas is
View SolutionAssertion: When ideal gas expand from P1,V1,T1, to P2,V2,T2 two steps, and work done is high in which number of steps are high
Reason: Work is path function
View SolutionA gas with cpcV=γ goes from an intial state (p1,V1,T1) to a final state (p2,V2,T2) through an adiabatic process. The work done by the gas is
View SolutionWhat is meant by (i) an adiabatic and (ii) an isothermal change of state of a gas. An ideal gas is expanded adiabatically from volume V1 to volume V2 is then compressed isothermally to its original volume V1 Draw the P-V curves representing the above changes. How will you show. in your graph the net work done by the gas?
View SolutionOne mole of an ideal gas is warmed slowly so that it goes form the PV state (PiVi) to (3Pi,3Vi) in such a way that the pressure of the gas is directly proportional to the volume.
(a) How much work is done on the gas in the process?
(b) How is the temperature of the gas related to its volume during this process?
View Solution
