The entropy change can be calculated by using the expression ΔS−qrevT. When water freezes in a glass beaker, choose the correct statement amongst the following:
ΔS (system) decreases but ΔS (surroundings) remains the same
ΔS (system) increases but ΔS (surroundings) decreases
ΔS (system) decreases but ΔS (surroundings) increases
ΔS (system) decreases but ΔS (surroundings) also decreases
The correct Answer is:C
To solve the question regarding the entropy change when water freezes in a glass beaker, we will analyze the situation step by step.
1. Understanding the Process:
- When water freezes, it undergoes a phase change from liquid to solid. During this process, the water loses heat to the surroundings.
2. Entropy of the System:
- The system in this case is the water. As water freezes, it becomes more ordered (solid state is more ordered than liquid state). Therefore, the randomness or disorder of the water decreases.
- This means that the entropy change for the system (ΔS_system) is negative, indicating a decrease in entropy.
3. Entropy of the Surroundings:
- As the water loses heat to the surroundings, the temperature of the surroundings increases. When the temperature of the surroundings increases, the randomness or disorder in the surroundings increases.
- Thus, the entropy change for the surroundings (ΔS_surrounding) is positive, indicating an increase in entropy.
4. Total Entropy Change:
- The total entropy change of the universe (ΔS_total) can be expressed as:
ΔStotal=ΔSsurrounding+ΔSsystem
- Since ΔS_system is negative and ΔS_surrounding is positive, for the total entropy change to be constant, the increase in ΔS_surrounding must be greater than the decrease in ΔS_system.
5. Conclusion:
- Therefore, when water freezes in a glass beaker, we conclude that:
- ΔS_system decreases (entropy of the system decreases).
- ΔS_surrounding increases (entropy of the surroundings increases).
- The correct statement is that the entropy of the system decreases while the entropy of the surroundings increases.
Final Answer:
The correct statement is: ΔS_system decreases and ΔS_surrounding increases.
---
- When water freezes, it undergoes a phase change from liquid to solid. During this process, the water loses heat to the surroundings.
- The system in this case is the water. As water freezes, it becomes more ordered (solid state is more ordered than liquid state). Therefore, the randomness or disorder of the water decreases.
- This means that the entropy change for the system (ΔS_system) is negative, indicating a decrease in entropy.
- As the water loses heat to the surroundings, the temperature of the surroundings increases. When the temperature of the surroundings increases, the randomness or disorder in the surroundings increases.
- Thus, the entropy change for the surroundings (ΔS_surrounding) is positive, indicating an increase in entropy.
- The total entropy change of the universe (ΔS_total) can be expressed as:
ΔStotal=ΔSsurrounding+ΔSsystem
- Since ΔS_system is negative and ΔS_surrounding is positive, for the total entropy change to be constant, the increase in ΔS_surrounding must be greater than the decrease in ΔS_system.
- Therefore, when water freezes in a glass beaker, we conclude that:
- ΔS_system decreases (entropy of the system decreases).
- ΔS_surrounding increases (entropy of the surroundings increases).
- The correct statement is that the entropy of the system decreases while the entropy of the surroundings increases.
The correct statement is: ΔS_system decreases and ΔS_surrounding increases.
Topper's Solved these Questions
Similar Questions
The pressure volume work for an ideal gas can be calculated by using the expression w=−∫vfViPexdV. The work can also be calculated from the pV-plot by using the area under the curve within the specified limits. When an ideal gas is compressed (a) reversibly or (B) irreversibly from volume Vi to Vf choose the correct option.
View SolutionFor an ideal gas, the work of reversible expansion under isothermal condition can be calculated by using expression =−nRTln.VfVi. A sample containing 1.0 mol of an ideal gas is expanded isothermally and reversible to ten times of its original volume, in two separate experiments. The expansion is carried out at 300 K and at 600 K respectively. Choose the correct option
View Solution
Knowledge Check
The pressure-volume work for an ideal gas can be calculated by using the expression W=−∫VfViPexdV. The work can also be calculated from the pV - plot by using the area under the curve within the specified limits. When an ideal gas is compressed (i) reversibly or (ii) irreversibly from volume Vi to Vf. Choose the correct option.
AWreversible=WirreversibleBWreversible<WirreversibleCWreversible>WirreversibleDWreversible=Wirreversible+PexΔV
As per second law of thermodynamics a process taken place spontaneously if and only if the entropy of the universe increases due to the process. Change in entropy is given by
ΔS=QrevT
What is the change in entropy of the universe due to the following reaction occuring at 27∘C ?
A+2B→C+2D,ΔH=+1.8kJmol−1
Molar entropy values of A, B, C and D are 1,2,3 and 4JK−1mol−1 respectively.
View SolutionThe thermodynamic property that measures the extent of molecular disorder is called entropy. Entropy change of phase transformation can be calculated using Trouton's formula (ΔS=ΔH/T). In the reversible adiabatic process, however, ΔS will be zero. the rise in temperature in isobaric and isochoric conditions is found to increase the randomness or entropy of the system.
ΔS=2.303Clog(T1/T2)
When 1 mol of an ideal gas is compressed to half of its volume, its temperature becomes half. Then the change in entropy (ΔS) would be
View SolutionThe thermodynamic property that measures the extent of molecular disorder is called entropy. Entropy change of phase transformation can be calculated using Trouton's formula (ΔS=ΔH/T). In the reversible adiabatic process, however, ΔS will be zero. the rise in temperature in isobaric and isochoric conditions is found to increase the randomness or entropy of the system.
ΔS=2.303Clog(T1/T2)
The entropy change in an adiabatic process is
View SolutionThe thermodynamic property that measures the extent of molecular disorder is called entropy. Entropy change of phase transformation can be calculated using Trouton's formula (ΔS=ΔH/T). In the reversible adiabatic process, however, ΔS will be zero. the rise in temperature in isobaric and isochoric conditions is found to increase the randomness or entropy of the system.
ΔS=2.303Clog(T1/T2)
The melting point of a solid is 200K and its latent heat of fusion is 400calmol−1. The entropy changes for the fusion of 1 mole of the solid (in cal K−1) at the same temperature would be
View SolutionEntropy is a state function and its value depends on two or three variable temperature (T), Pressure(P) and volume (V). Entropy change for an ideal gas having number of moles(n) can be determined by the following equation.
ΔS=2.303nCvlog(T2T1)+2.303nR log(V2V1)
ΔS=2.303nCPlog(T2T1)+2.303nR log(P1P2)
Since free energy change for a process or a chemical equation is a deciding factor of spontaneity , which can be obtained by using entropy change (ΔS) according to the expression, ΔG=ΔH−TΔS at a temperature T
What would be the entropy change involved in thermodynamic expansion of 2 moles of a gas from a volume of 5 L to a volume of 50 L at 25∘ C [Given R=8.3J/mole−K]
View SolutionFor a sponaneous reaction, the free energy change must be negative, ΔG=ΔH−TΔS,ΔH is the enthalpy change during the reaction. T is the absolute temperature, and ΔS is the change in entropy during the reaction. Consider a reaction such as the formation of an oxide
M+O2→MO
Dioxygen is used up in the course of this reaction. Gases have a more random structure (less ordered) than liquid or solids. Consequently gases have a higher entropy than liquids and solids. In this reaction S (entropy or randomness) decreases, hence ΔS is negative. Thus, if the temperature is raised then TΔS becomes more negative,Since, TΔS is substracted in the equation, then ΔG becomes less negative. Thus, the free energy change increases with the increase in temperature.
The free energy changes that occur when one mole of common reactant (in this case dioxygen) is used may be plotted graphically aginst temperature for a number of reactions of metals to their oxides. The following plot is called an Ellingham diagram for metal oxide. Understanding of Ellingham diagram is extremely important for the efficient extraction of metals.
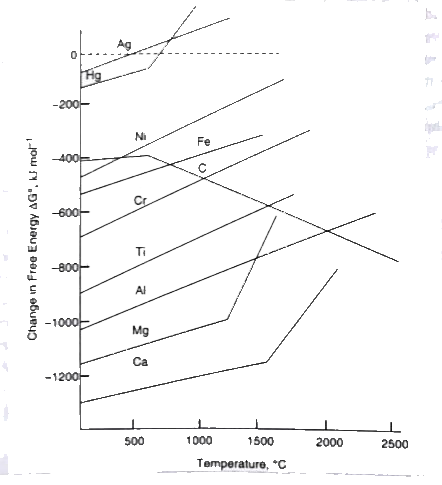
Which of the following elements can be prepared by heating the oxide above 400∘C ?
View SolutionFor a sponaneous reaction, the free energy change must be negative, ΔG=ΔH−TΔS,ΔH is the enthalpy change during the reaction. T is the absolute temperature, and ΔS is the change in entropy during the reaction. Consider a reaction such as the formation of an oxide
M+O2→MO
Dioxygen is used up in the course of this reaction. Gases have a more random structure (less ordered) than liquid or solids. Consequently gases have a higher entropy than liquids and solids. In this reaction S (entropy or randomness) decreases, hence ΔS is negative. Thus, if the temperature is raised then TΔS becomes more negative,Since, TΔS is substracted in the equation, then ΔG becomes less negative. Thus, the free energy change increases with the increase in temperature.
The free energy changes that occur when one mole of common reactant (in this case dioxygen) is used may be plotted graphically aginst temperature for a number of reactions of metals to their oxides. The following plot is called an Ellingham diagram for metal oxide. Understanding of Ellingham diagram is extremely important for the efficient extraction of metals.
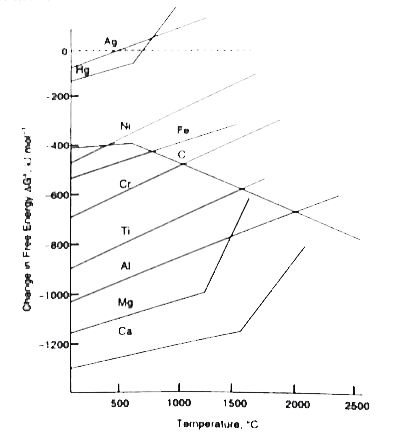
For the conversion of Ca(s) to Ca(s) which of the following represent the ΔG vs. T ?
View Solution
