Out of aphelion and perihelion, where is the speed of the earth more and why ?
To determine where the speed of the Earth is greater, we need to analyze the positions of the Earth in its elliptical orbit around the Sun, specifically at aphelion and perihelion.
1. Understanding the Terms:
- Aphelion: This is the point in Earth's orbit where it is farthest from the Sun.
- Perihelion: This is the point in Earth's orbit where it is closest to the Sun.
2. Kepler's Laws of Planetary Motion:
- According to Kepler's Second Law (the Law of Areas), a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. This implies that the planet moves faster when it is closer to the Sun and slower when it is farther away.
3. Analyzing Speeds at Aphelion and Perihelion:
- At perihelion (point P), the Earth is closer to the Sun, which means it will move faster due to the stronger gravitational pull from the Sun.
- At aphelion (point A), the Earth is farther from the Sun, resulting in a weaker gravitational pull and therefore a slower speed.
4. Conclusion:
- The speed of the Earth is greater at perihelion than at aphelion. This can be summarized as:
- Vp>Va
- Where Vp is the speed at perihelion and Va is the speed at aphelion.
Final Answer:
The speed of the Earth is greater at perihelion because it is closer to the Sun, resulting in a stronger gravitational force that increases its orbital speed.
---
- Aphelion: This is the point in Earth's orbit where it is farthest from the Sun.
- Perihelion: This is the point in Earth's orbit where it is closest to the Sun.
- According to Kepler's Second Law (the Law of Areas), a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. This implies that the planet moves faster when it is closer to the Sun and slower when it is farther away.
- At perihelion (point P), the Earth is closer to the Sun, which means it will move faster due to the stronger gravitational pull from the Sun.
- At aphelion (point A), the Earth is farther from the Sun, resulting in a weaker gravitational pull and therefore a slower speed.
- The speed of the Earth is greater at perihelion than at aphelion. This can be summarized as:
- Vp>Va
- Where Vp is the speed at perihelion and Va is the speed at aphelion.
The speed of the Earth is greater at perihelion because it is closer to the Sun, resulting in a stronger gravitational force that increases its orbital speed.
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GRAVITATIONEXERCISE - Short Answer type question
6 Videos
- GRAVITATIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GRAVITATIONEXERCISE - Long Answer type question
5 Videos
- GRAVITATIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GRAVITATIONEXERCISE - Long Answer type question
5 Videos
- KINETIC THEORYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Multiple Choice Questions (MCQs)
31 Videos
Similar Questions
A satellite is in an elliptical orbit around the earth with aphelion of 6R and perihelion of 2R where R=6400km is the radius of the earth. Find eccentricity of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a circular orbit of radius 6R? [G=6.67×10−11SI units and M=6×1024kg]
View SolutionWhich out of helium and neon would adsorb on the surface of charcoal more readily and why?
View Solution
Knowledge Check
An artificial satellite is in an elliptical orbit around the earth with aphelion of 6R and perihelion of 2R where R is radius of the earth =6400km. Calculate the eccentricity of the elliptical orbit.
A12B13C14D16
A satellite of mass m orbits the earth in an elliptical orbit having aphelion distance ra ad perihelion distance rp. The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are a and b respectively. The angular momentum of the satellite is
View SolutionThe Earth has a circular orbit of radius r and period t around the sum, Mars has a circular orbit of radius R and period T. In order to send a spacecraft from the Earth to Mars, it is convenient to launch the spacecraft inot an elliptical orbit whose perihelion coincides with the orbit of the Earth and whose aphelion coincides with the orbit of Mars, this orbit requires the least amount of energy for a trip to Mars. The time t' taken by a spacecraft to reach Mars from the Earth satisfies:
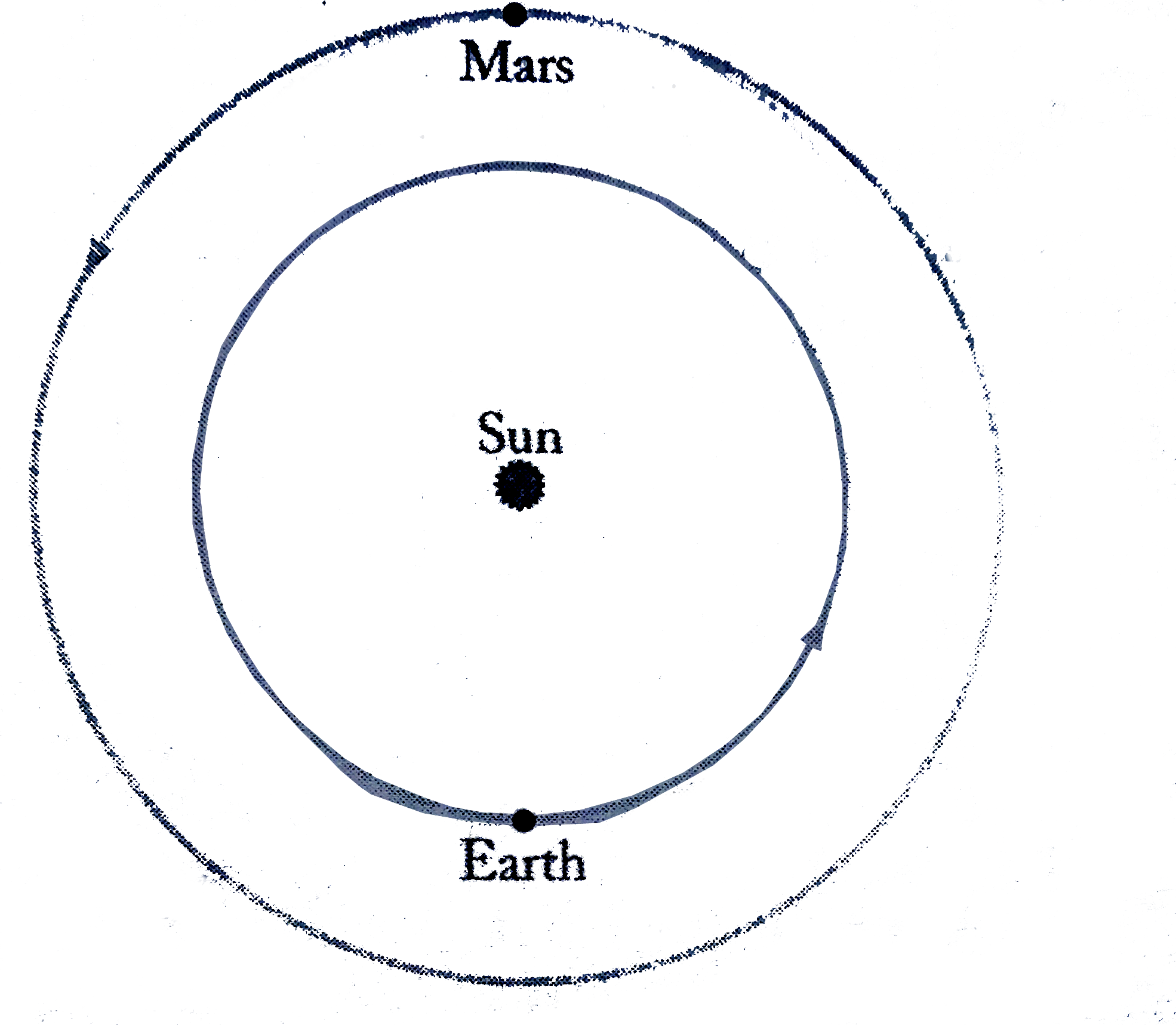
View SolutionConsider a satellite orbiting the earth as shown in the figure below. Let LaandLp represent the angular momentum of the satellite about the earth when at aphelion and perihelion respectively. Consider the following relations

(i) La=Lp
(ii) La=−Lp
(iii) ra×La=rp×Lp
Which of the above relation(s) is/are true ?
View SolutionWhy does a body lose weight at the centre of the earth?
View SolutionThe escape speed of a body from the earth depends upon
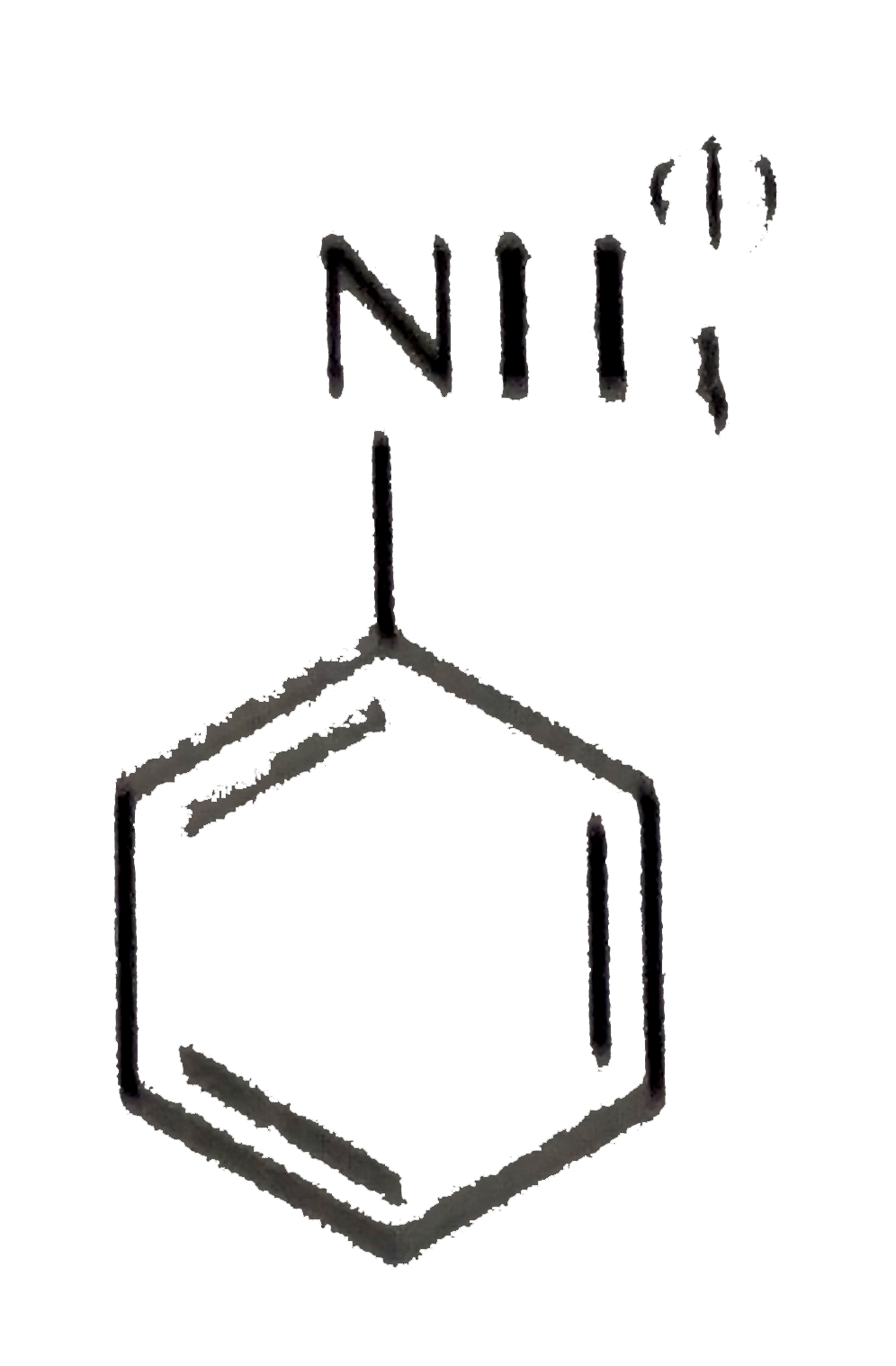
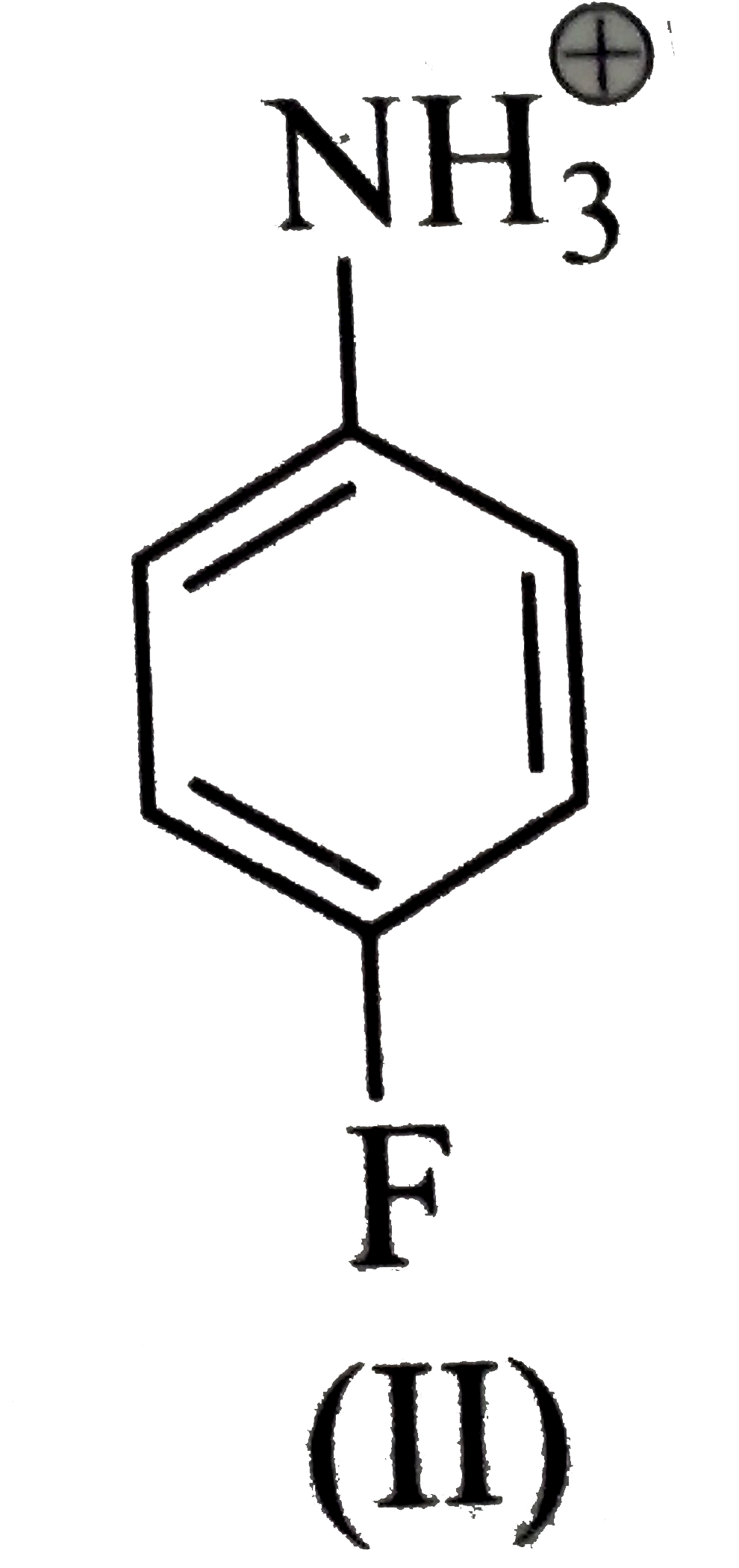
View SolutionWhich of the following is more acidic and why ?
View SolutionWhich one is more stable and why?

View Solution
