Calculate the work done by a car against gravity in moving along a straight horizontal road. The mass of the car is 400 kg and the distance moved is 2m.
To calculate the work done by a car against gravity while moving along a straight horizontal road, we can follow these steps:
Step 1: Identify the Forces Involved
The main force acting against gravity is the weight of the car, which can be calculated using the formula:
F=mg
where:
- m is the mass of the car (400 kg)
- g is the acceleration due to gravity (approximately 9.81m/s2)
Step 2: Calculate the Weight of the Car
Using the values provided:
F=400kg×9.81m/s2
F=3924N
Step 3: Determine the Displacement
The displacement of the car is given as 2 meters. However, since the car is moving horizontally, we need to consider the angle between the force (weight acting downwards) and the displacement (horizontal movement).
Step 4: Calculate the Work Done
The work done (W) against gravity can be calculated using the formula:
W=F⋅d⋅cos(θ)
where:
- F is the force (weight of the car)
- d is the displacement (2 m)
- θ is the angle between the force and the displacement
In this case, since the force of gravity acts vertically downwards and the displacement is horizontal, the angle θ is 90 degrees. Therefore:
cos(90∘)=0
Substituting the values into the work done formula:
W=3924N×2m×cos(90∘)
W=3924N×2m×0
W=0J
Conclusion
The work done by the car against gravity while moving along a straight horizontal road is 0J.
---
The main force acting against gravity is the weight of the car, which can be calculated using the formula:
F=mg
where:
- m is the mass of the car (400 kg)
- g is the acceleration due to gravity (approximately 9.81m/s2)
Using the values provided:
F=400kg×9.81m/s2
F=3924N
The displacement of the car is given as 2 meters. However, since the car is moving horizontally, we need to consider the angle between the force (weight acting downwards) and the displacement (horizontal movement).
The work done (W) against gravity can be calculated using the formula:
W=F⋅d⋅cos(θ)
where:
- F is the force (weight of the car)
- d is the displacement (2 m)
- θ is the angle between the force and the displacement
cos(90∘)=0
W=3924N×2m×cos(90∘)
W=3924N×2m×0
W=0J
The work done by the car against gravity while moving along a straight horizontal road is 0J.
Similar Questions
Consider, a car moving along a straight horizontal road with a speed of 72 km/h. If the coefficient of static friction between the tyre and the road is 0.5, the shortest distance in which the car can be stopped is (Take g=10/s2)
View Solutiona. A rail road flat car of mass M can roll without friction along a straight horizontal track . Initially, a man of mass m is standing on the car which is moving to the right with speed v0. What is the change in velocity of the car if the man runs to the left so that his speed relative to the car is vrel just before he jumps off at the left end?
b. If there are n men each of mass m on the car, should they all run and jump off together or should they run and jump one by one in order to give a greater velocity to the car?

View Solution
Knowledge Check
A car moving on a straight road is an example of:
Arotatory motionBrectilinear motionCoscillatory motionDperiodic motionA car moving on a horizontal road may be thrown out of the road in taking a turn
Aby the gravitational forceBdue to the lack of proper centripetal forceCdue to the rolling frictional force between the tyre and roadDdue to the reaction of the ground
Consider a car moving on a straight road with a speed of 100m/s. The distance at which car can be stopped is [μk=0.5]
View SolutionConsider a car moving on a straight road with a speed of 100m/s. The distance at which car can be stopped is [μk=0.5]
View SolutionIn order to stop a car in shortest distance on a horizontal road one should
View SolutionA car is moving along a straight horizontal road with a speed v0 . If the coefficient of friction between the tyres and the road is μ , the shortest distance in which the car can be stopped is
View SolutionThe velocity-time graph of a car moving along a straight road is shown in figure. The average velocity of the car is first 25 seconds is
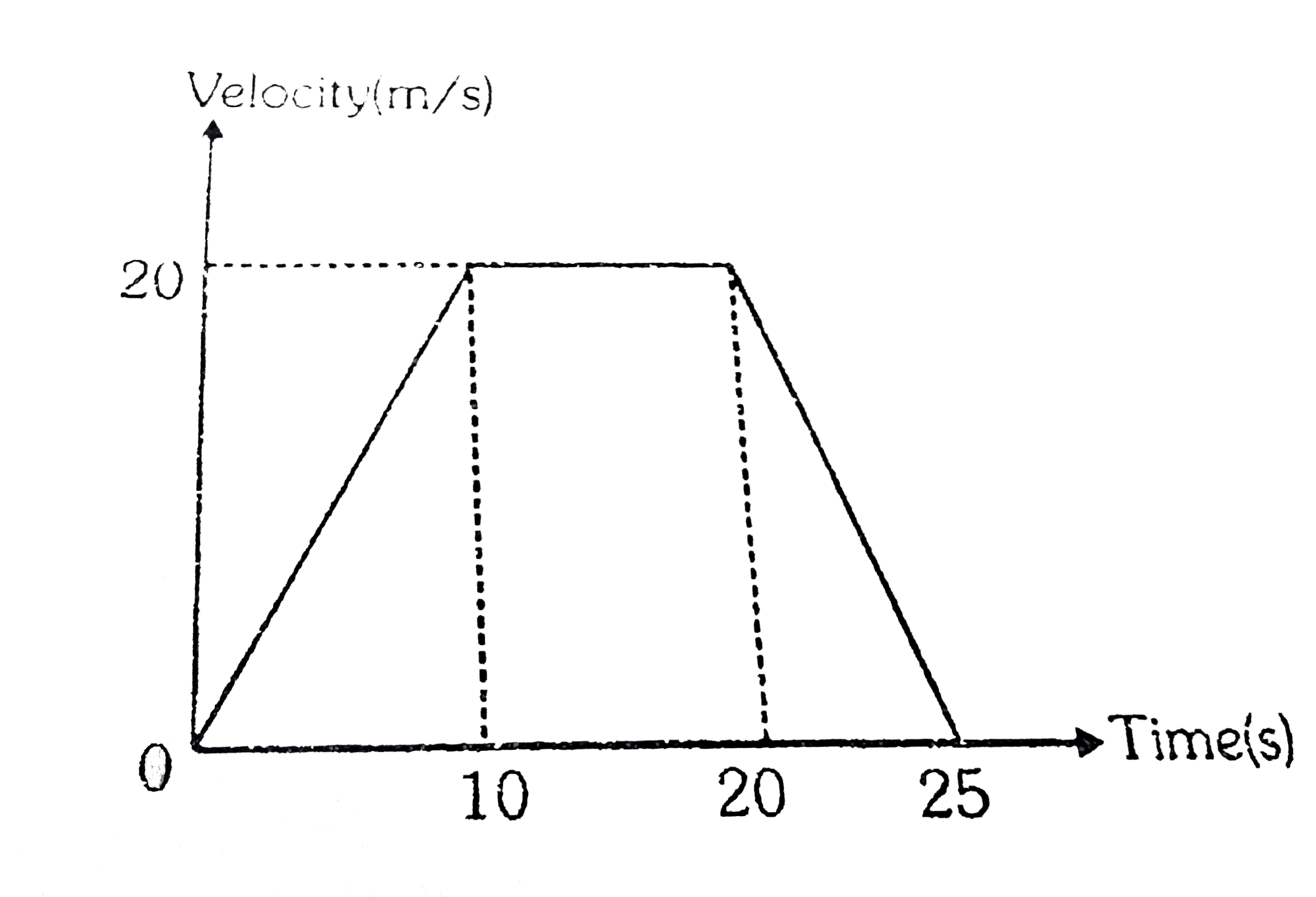
View SolutionThe velocity-time graph of a car moving along a straight road is shown in figure. The average velocity of the car in first 25 seconds is
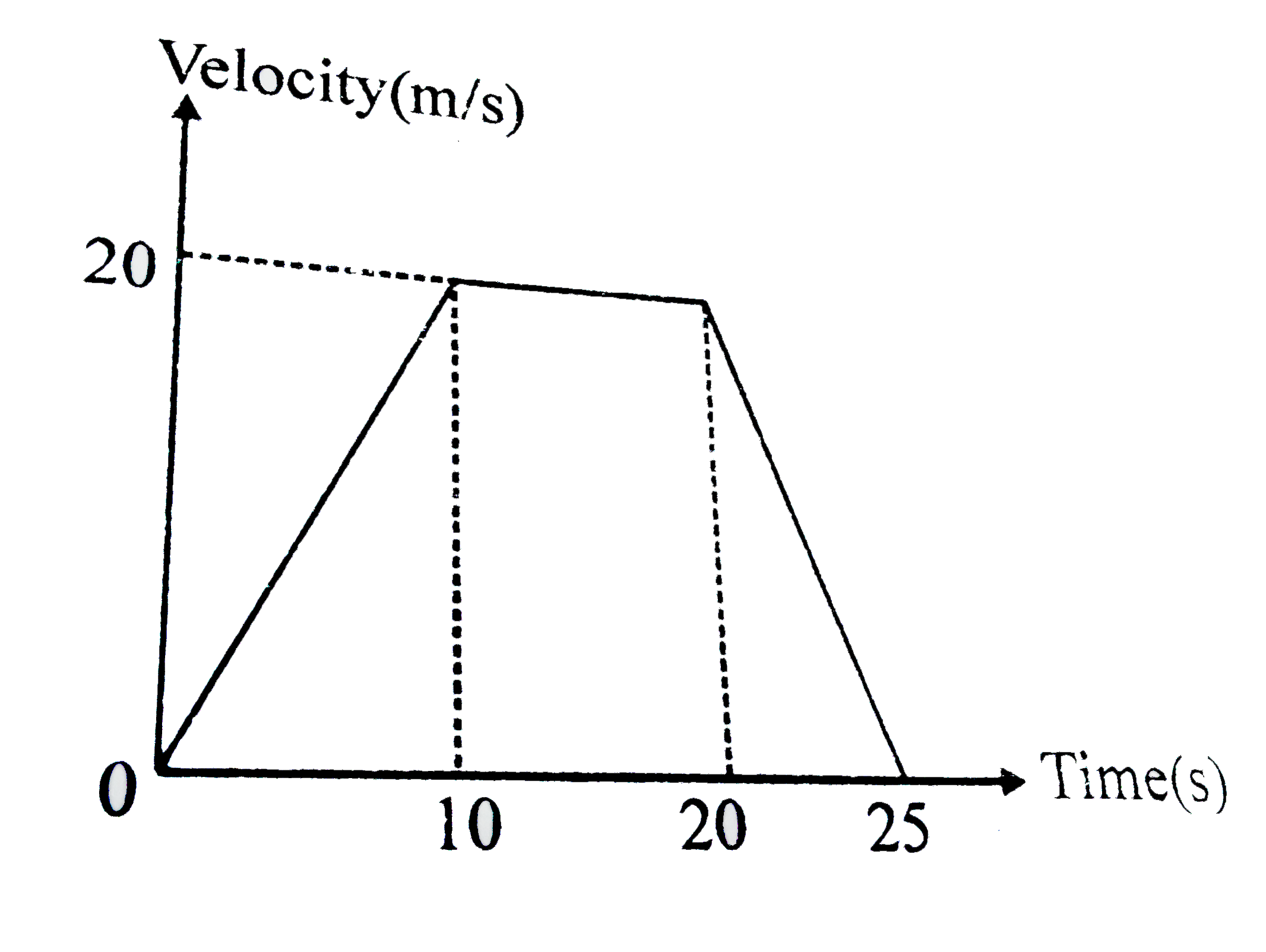
View Solution