यदि दो सरल आवर्त गतियों के विस्थापान $y_{1} = 10 sin [3 π t + \frac{π}{4}]$ और $y_{2} = 5 [sin (3 π t) + \sqrt{3} cos (3 π t)]$ है।

Video Solution

Text Solution

Verified by Experts

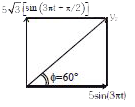
$∵ y_{2} = 5 [sin (3 π t) + \sqrt{3} cos (3 π t)]$ है

$∴$ यदि $5 - A cos ϕ$

और $5 \sqrt{3} = A sin ϕ$ हो

तो $A = \sqrt{5^{2} + {(5 \sqrt{3})}^{2}} = 10$

और $tan ϕ = \frac{5 \sqrt{3}}{5} = \sqrt{3}$ अतः $ϕ = \frac{π}{3}$

समीकरण (i) से

$y_{2} - A cos ϕ sin (3 π t) + A sin ϕ cos (3 π t)$

$\Rightarrow y_{2} = A sin (3 π t + ϕ)$

लेकिन $y_{2} = 10 sin [3 π t + (\frac{π}{3})] < b r > < b r >$ अतः $\frac{A_{1}}{A_{2}} = \frac{10}{10} A_{1} : A_{2} = 1 : 1$

कलांतर $= \frac{π}{3} - \frac{π}{4} = \frac{π}{12}$

Updated on:21/07/2023

|

Class 12 PHYSICS दोलन

Topper's Solved these Questions

Similar Questions

ALLEN HINDI-दोलन -EXERCISE-IV

Home
Ask Doubt
Profile