→r=0.5ˆj−2ˆk पर एक कण पर बल →F=2ˆi−3ˆk कार्यरत है तो उस बिंदु के सापेक्ष जिसके निरेशांक है, (2.0m,0,−3.0m) →τ होगा
(−3.0ˆi−4.5ˆj−ˆk)N−m
(3ˆi+6ˆj−ˆk)N−m
(−20ˆi+4.0ˆj−ˆk)N−m
(−1.5ˆi−4.0ˆj−ˆk)N−m
The correct Answer is:D
Step by step video, text & image solution for vec(r )= 0.5 hat(j) - 2hat(k) पर एक कण पर बल vec(F)= 2hat(i) - 3hat(k) कार्यरत है तो उस बिंदु के सापेक्ष जिसके निरेशांक है, (2.0 m, 0, -3.0m) " " vec(tau) होगा by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- घूर्णन गति Book:ALLEN HINDIChapter:घूर्णन गति Exercise:EXERCISE - II (Previous Year Questions)
Explore 26 Videos
- घूर्णन गति Book:ALLEN HINDIChapter:घूर्णन गति Exercise:EXERCISE - III (Analytical Questions)
Explore 7 Videos
- घूर्णन गति Book:ALLEN HINDIChapter:घूर्णन गति Exercise:BEGINNER.S BOX - 6
Explore 5 Videos
- गुरुत्वाकर्षण Book:ALLEN HINDIChapter:गुरुत्वाकर्षण Exercise:EXERCISE -IV (ASSERTION & REASON)
Explore 21 Videos
- तरंग गति तथा डॉप्लर प्रभाव Book:ALLEN HINDIChapter:तरंग गति तथा डॉप्लर प्रभाव Exercise:EXERCISE-IV (Assertion & Reason)
Explore 34 Videos
Similar Questions
चित्रों में दिखाए गए संभावित प्रतिरूपों में अगर एक द्रव्यमान की स्ट्रीट लाइट को एक लम्बाई की एकसमान छड़ी के एक सिरे से लटकाया गया है, तो :-
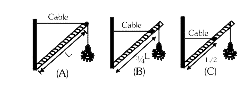
View Solutionएक 500 N भार की सीढ़ी एक घर्षणविहीन दीवार के सहारे इस प्रकार रखी है कि सीढ़ी का ऊपरी सिरा क्षैतिज से 6 मीटर ऊपर एवं दीवार से निचला सिरा 4 मीटर की दूरी पर है। यदि द्रव्यमान केन्द्र निचले सिरे से एक तिहाई दूरी पर हो, तो दीवार की प्रतिक्रिया (न्यूटन में) होगी :
View Solutionh ऊंचाई के आनत तल के शीर्ष से एक वलय, चकती तथा गोले को लुढ़कने के लिए एक साथ छोड़ा जाता है । इनके तल पर पहुचने का क्रम लिखिए ?
View Solutionकथन : पृथ्वी के ध्रुव एवं विषुवत रेखा के मध्य गुरूत्वीय त्वरण के मान में अन्तर, पृथ्वी के कोणीय वेग के वर्ग के समानुपाती होता है।
कारण : गुरूत्वीय त्वरण का मान विषुवत रेखा पर न्यूनतम और ध्रुव पर अधिकतम होता है।
View Solutionकथन : अप्रगामी तरंग प्रारूप में दो क्रमागत निस्पंदों के बीच माध्यम के कण समान कला में एवं भिन्न-भिन्न आयाम से कम्पन करते हैं।
कारण : अप्रगामी तरंग में, कम्पनों का आयाम कणों की स्थिति पर निर्भर नही करता है।
View Solution→a=2ˆi−ˆj+ˆk,→b=ˆi+2ˆj−ˆk,→c=ˆi+ˆj−2ˆk. A vector coplanar with →band→c whose projectin on →a is magnitude √23 is 2ˆi+3ˆj−3ˆk b. −2ˆi−ˆj+5ˆk c. 2ˆi+3ˆj+3ˆk d. 2ˆi+ˆj+5ˆk
View Solutionif vec a=2hat i-3hat j+hat k and vec b=hat i+2hat j-3hat k then find vec axvec b
View SolutionIf vec a=2hat i+2hat j+3hat k,vec b=-hat i+2hat j+hat k and vec c=3hat i+hat j then vec a+tvec b is perpendicular to vec c if t=
View SolutionIf quad 3hat i+2hat j-5hat k,vec a=2hat i-hat j+hat k,vec b=hat i+3hat j-2hat k,vec c=-2hat i+hat j-3hat k such that vec r=lambdavec a+muvec b+gammavec c, then
View SolutionIf vec a=2hat i+hat j+hat k,vec b=3hat i-4hat j+2hat k and vec c=hat i-2hat j+2hat k then the projection of vec a+vec b is
View Solutionvec(A)=hat(j)-2hat(i)+3hat(k) " , "vec(B)= hat(i)+2hat(j)+2hat(k) find vec(A).vec(B)
View SolutionFind [→a→b→c], when
(i)→a=2ˆi+ˆj+3ˆk,→b=−ˆi+2ˆj+ˆkand→c=3ˆi+ˆj+2ˆk
(ii) →a=2ˆi−3ˆj+4ˆk,→b=ˆi+2ˆj−ˆkand→c=3ˆi−ˆj+2ˆk
(iii) →a=2ˆi−3ˆj,→b=ˆi+ˆj−ˆkand→c=3ˆi−ˆk
View SolutionShow that the vectors →a,→b,→c are coplanar, when
(i) →a=ˆi−2ˆj+3ˆk,→b=−2ˆi+3ˆj−4ˆkand→c=ˆi−3ˆj+5ˆk
(ii) →a=ˆi+3ˆj+ˆk,→b=2ˆi−ˆj−ˆkand→c=7ˆj+3ˆk
(iii) →a=2ˆi−ˆj+2ˆk,→b=ˆi+2ˆj−3ˆkand→c=3ˆi−4ˆj+7ˆk
View SolutionFind the shortest distance between the given line
→r=(ˆi+ˆj)+λ(2ˆi−ˆj+ˆk)
→r=(2ˆi+ˆj−ˆk)+μ(3ˆi−5ˆj+2ˆk)
View SolutionIf →a=2ˆi+3ˆj−ˆk,→b=3ˆi+5ˆj+2ˆk,→c=−ˆi−2ˆj+3ˆk,
→a(→a×→b)=(→a⋅→c)→b−(→a⋅→b)→c
View Solution→a.(→b×→c) ज्ञात कीजिए यदि →a=2ˆj+ˆi+3ˆk,→a+3ˆk+ˆj और →c=3ˆj+ˆi+2ˆk है।
View Solution